光的干涉
本文中我们将研究光的干涉现象。
两束波的干涉条件
若几束光的叠加产生的辐照度不等于其辐照度之和,那么我们称这几束光发生了干涉。 叠加的辐照度减去辐照度之和的差称为其干涉项。 若两束光发生干涉,那么称它们为相干的;相对地,若不发生干涉,那么称它们为不相干的。
单色光的干涉条件
我们先考虑单色光的干涉,此时所有光都可以视为正弦波。
两束单色光能发生干涉,当且仅当其频率相等。
我们设两束波可以写为: \(s_i (M,t) = A_i(M) \cos (\omega_i t - \varphi_i(M))\) 首先,我们有: \(\mathcal E(M) = k \langle s^2 \rangle_T = k \langle (s_1+s_2)^2\rangle_T = k \langle s_1^2\rangle_T + k \langle s_2^2 \rangle_T + 2k \langle s_1 s_2 \rangle_T\) 从而我们需要研究$\langle s_1 s_2 \rangle$。 \(\begin{aligned} \langle s_1 s_2 \rangle _T &= \langle A_1(M) A_2(M) \cos(\omega_1 t - \varphi_1(M)) \cos(\omega_2 t - \varphi_2(M)) \rangle \\ &= A_1(M) A_2(M) \langle \cos((\omega_1 + \omega_2)t - (\varphi_1 + \varphi_2)) + \cos ((\omega_1 - \omega_2)t - (\varphi_1 - \varphi_2)) \rangle \\ \end{aligned}\) 当$T \gg \tau$时,即当传感器的响应时间远大于波的周期时,可以认为$\cos ((\omega_1 + \omega_2) t)$为零。 从而,当且仅当$\omega_1 = \omega_2$时,这个值是一个稳定的常量,可以观察到干涉现象。
值得注意的是,当两个波的频率非常接近但不相同时,也可以观测到干涉现象,但是由于时变的特点,这种现象不能稳定地存在。
准单色光的干涉条件
现实中,我们不可能产生完美的单色光。 相对地,我们产生的几乎都是准单色光,这种光源并不发出一个连续的正弦波,而是不间断地发出振幅和频率相等,持续时间固定的波包。 波包的持续时间称为光源的相干时间$\tau_c$,相干时间乘波速称为其相干长度$\mathcal l_c$。
波包的初相位是随机的,这就使得准单色光的干涉具有额外的条件。
两束准单色光相干,当且仅当其频率相等,且其相位差相等或变化缓慢。
我们要求两束准单色光的相位差相等,因此其随机的初相位必须相等,这就相当于要求准单色光必须从一个光源发出。
分波前与分振幅干涉
正如前文所述,准单色光的干涉要发生,那么其一定来自同一个光源,因此我们必须使用某种方法将一个光源的光分成两份。 如果发生干涉的光是来自同一光源的不同光束,那么这种干涉称为分波前干涉; 如果发生干涉的光来自同一光束,且经过分光镜发生干涉,那么这种干涉称为分振幅干涉。
光程差约束
正如前文所述,准单色光以波包的形式发生干涉,这些波包的初相位各不相同。 因此,为了发生干涉,干涉点处两束光必须位于同一个波包内,这就提出了对光程差的约束。
两个波包同时到达点$M$,若: \(|\mathcal L(S_1M) - \mathcal L(S_2M)| < \mathcal l\_c\)
总结
来自同一个光源的两束准单色光能够发生干涉,当且仅当其频率相等,且干涉发生处的光程差不超过相干长度。 若发生干涉,那么干涉之后的辐照度为: \(\mathcal E(M) = \mathcal E_1(M) + \mathcal E_2(M) + 2 \sqrt{\mathcal E_1(M) \mathcal E_2(M)} \cos(\varphi_2(M) - \varphi_1(M))\) 如果写成光程差的形式,那么有: \(\mathcal E(M) = \mathcal E_1(M) + \mathcal E_2(M) + 2 \sqrt{\mathcal E_1(M) \mathcal E_2(M)} \cos(\frac{2\pi}{\lambda_0} \delta(M))\) 其中$\delta(M) = \mathcal L(S_2M) - \mathcal L(S_1M)$。 注意存在三种情况会导致额外的$\pi$相位差,从而光程差具有一个额外的半波长。
正如我们在波动物理中所学的,干涉后的辐照度也可以用复数相加的形式表示出来。
其他状态参量
本节中,我们将研究一些用来描述干涉的额外参量。
在本节中,我们假设在传感器的尺度上,$\mathcal E_1(M)$和$\mathcal E_2(M)$变化不明显,因此我们直接设它们为常量,从而有: \(\mathcal E(M) = \mathcal E_1 + \mathcal E_2 + 2 \sqrt{\mathcal E_1 \mathcal E_2} \cos(\Delta \varphi_{2/1}(M))\) 其中$\Delta \varphi_{2/1}(M) = \varphi_2(M) - \varphi_1(M)$
干涉条纹
根据此前的说明,不难发现干涉产生的光强与位置和对应的相位差有关。 若相位差为$0$,那么干涉光强取极大值,记为$\mathcal E_{max} = (\sqrt{\mathcal E_1} + \sqrt{\mathcal E_2})^2$,此时称为干涉相长; 若相位差为$\pi$,那么干涉光强取极小值,记为$\mathcal E_{min} = (\sqrt{\mathcal E_1} - \sqrt{\mathcal E_2})^2$,此时称为干涉相消。
我们称干涉产生的光强相同的一块连通的区域为干涉条纹,无论这个区域是否真的是一个条纹。 在干涉相消的位置的干涉条纹称为暗条纹,而在干涉相长的位置的称为亮条纹。
干涉阶数
称$M$点处的干涉阶数,记为$p(M)$,为: \(p(M) = \frac{\Delta \varphi(M)}{2 \pi} = \frac{\delta_\text{opt} (M)}{\lambda_0}\) 其中$\delta_\text{opt}$表示考虑三种特殊情况导致的额外相位差后的光程差。
设$m$为一整数,则亮条纹处满足: \(\begin{multline} \Delta \varphi(M) = m 2 \pi \\ \iff p(M) = m \\ \iff \delta_\text{opt}(M) = m \lambda_0 \end{multline}\) 暗条纹处满足: \(\begin{multline} \Delta \varphi(M) = (2m+1) \pi \\ \iff p(M) = m + \frac{1}{2} \\ \iff \delta_\text{opt}(M) = (m + \frac{1}{2})\lambda_0 \end{multline}\)
对比度
称干涉图案的对比度$\Gamma$为一个实数: \(\Gamma = \frac{\mathcal E_\text{max} - \mathcal E_\text{min}}{\mathcal E_\text{max} + \mathcal E_\text{min}}\) 这个实数表征了干涉条纹的明显程度。
对于两束波干涉的情况,对比度通常使用以下式子算出: \(\Gamma = \frac{2 \sqrt{\mathcal E_1 \mathcal E_2}}{\mathcal E_1 + \mathcal E_2}\)
有限远处点光源的干涉
干涉图样
设两个相干的点光源$S_1,S_2$放置在折射率为$n$的均匀介质之中,两者之间的距离有限,那么干涉条纹形成沿$S_1S_2$轴旋转的旋转双曲面图样。 这种干涉是非定域的,因为可在空间中任何一点观察到干涉现象,且干涉现象的对比度与位置无关。 当且仅当光屏平行于或正交于轴$S_1S_2$时,才可观察到干涉条纹,前者所见的干涉条纹为双曲线,光屏较小时可近似为直线,后者所见的为圆。
为了简化我们的研究,接下来我们提出一个引理用来化简计算。
记$I$为$S_1$和$S_2$两点之间的中点,$M$为距离光源非常远一点,那么有: \(S_2M - S_1M = \vec{S_2S_1} \cdot \frac{\vec{IM}}{|IM|}\)
我们考虑计算$S_2M^2 - S_1M^2$: \(\begin{aligned} S_2M^2 - S_1M^2 &= (\vec{S_2M} + \vec{S_1M})(\vec{S_2M} - \vec{S_1M}) \\ &= (\vec{S_2I} + \vec{IM} + \vec{S_1I} + \vec{IM})(\vec{S_2M} - \vec{S_1M}) \\ &= 2\vec{IM} \cdot (\vec{S_2M} - \vec{S_1M}) \\ &= 2 \vec{IM} \cdot \vec{S_2S_1}\end{aligned}\) 又有: \(\begin{aligned} S_2M^2 - S_1M^2 &= (|S_2M| + |S_1M|)(|S_2M| - |S_1M|) \\ &\approx 2|IM|(|S_2M| - |S_1M|) \end{aligned}\) 左右相等,从而原命题得证。
直线干涉图样
设光屏平行于两个有限远处的点光源连成的直线放置,距点光源的距离为$D$。 两点光源的连线在光屏上的投影记为Y轴,中点$I$在光屏上的投影(即中垂线与平面的交点)记为原点。 两光源之间的距离为$a$,且远小于$D$,那么在原点附近的点处,从两个点光源出发到光屏上一点的光程差为: \(\delta = \mathcal L(S_2M) - \mathcal L(S_1M) = n \frac{ay}{D}\)
记得光程差和相位差满足:
\(2 \pi \delta = \lambda_0 \Delta \varphi\)
这样的光程差形成直线型的干涉图样,如下图所示。

两个条纹之间的间距为常数,满足: \(i = \frac{\lambda_0 D}{na} = \frac{\lambda D}{a}\)
有: \(\begin{aligned} S_2M - S_1M &= \vec{S_2S_1} \cdot \vec u &(根据几何引理) \\ &= \frac{ay}{IM} \\ &\approx \frac{ay}{D} \end{aligned}\)
环状干涉图样
若光屏垂直于两个点光源的连线放置,此时我们设点光源的中点$I$到光屏的距离为$D$,光屏的原点为中点在光屏上的投影(或光源的投影,这两者是重合的)。 此时光程差满足: \(\delta = \mathcal L (S_2M) - \mathcal L(S_1M) = na \cos i \approx na (1 - \frac{r^2}{2D^2})\) 其中$i$表示光屏上的点$M$到中点$I$的连线与点光源连线的夹角,$r$表示$M$到原点的位置。
这样的光程差会形成同心圆环形状的干涉图样,但是圆环之间的间距不是常数。
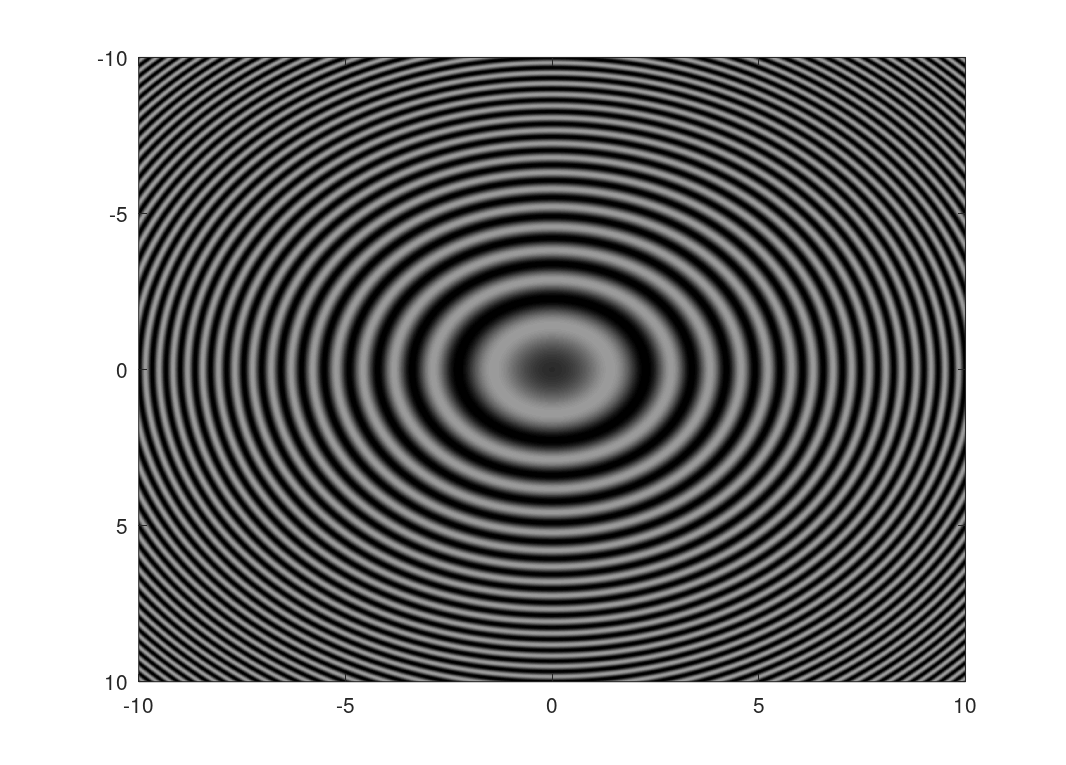
无穷远处点光源的干涉
当点光源位于无穷远处时,其发射的光可以认为是一束无限大小的平行光。 我们直接把其发射光近似为一个平面波: \(s_i(M,t) = A_{0i} \cos (\omega t \underbrace{- \varphi_i(O) - \vec k_i \cdot \vec{OM}}_{-\varphi_i(M)})\) 其中$O$为任选的参考点,或原点。
设光在折射率为$n$的介质中传播,那么有 \(\Vert \vec k_1 \Vert = \Vert \vec k_2 \Vert = n \frac{2\pi}{\lambda_0} = k\)
干涉图样
无穷远处点光源的干涉图样是和两点光源所成角的角平分线平行的直线条纹。 条纹之间的距离相等,满足: \(i = \frac{\lambda}{2 \sin (\frac{\alpha}{2})} = \frac{\lambda_0}{2n \sin(\frac{\alpha}{2})}\) 其中$\alpha$为两点光源所成的角度。
从平面上任取一点作为原点$O$,设X轴与两光束的角平分线平行。 首先,有: \(\Delta \varphi(M) = \varphi_2(M) - \varphi_1(M) = (\vec k_2 - \vec k_1) \cdot \vec{OM} + \varphi_2(O) - \varphi_1(O)\) 然后,我们把$\vec k$正交分解,可得: \(\begin{aligned} \vec k_1 &= \frac{2n\pi}{\lambda_0} (\sin \frac{\alpha}{2} (- \vec e_y) + \cos \frac{\alpha}{2} \vec e_x) \\ \vec k_2 &= \frac{2n\pi}{\lambda_0} (\sin \frac{\alpha}{2} (\vec e_y) + \cos \frac{\alpha}{2} \vec e_x) \end{aligned}\) 从而: \(\vec k_2 - \vec k_1 = 2 k \sin \frac{\alpha}{2} \vec e_y\) 从而: \(\Delta \varphi(M) = 2 k \sin \frac{\alpha}{2} y_{OM} + \varphi_2(O) - \varphi_1(O)\) 只要$y_{OM}$相同,那么相位差就相同,因此与X轴平行的直线的光强是相同的,从而形成条纹状的干涉图样。 另一方面,设第$q$阶干涉的Y坐标为$y_q$,那么有: \(2 \pi q = 2 k \sin \frac{\alpha}{2} y_q + C\) 从而 \(i = \frac{2\pi}{2k \sin\frac{\alpha}{2}} = \frac{\lambda_0}{2 n \sin \frac{\alpha}{2}}\)