动力学与基本定理

表述运动

当我们描述物体，尤其是连续体的运动时，通常可以采用两种视点：拉格朗日视点和欧拉视点。

在拉格朗日法中，连续体被视作一些微小粒子的集合，这些微小粒子的性质随着时间发生各种变化。 在这种表述中，连续体的任意性质只随着时间变化而变化，通常在对时间求导时写成全导数的形式。

在欧拉法中，我们不对从哪个位置观测连续体做任何假设，因此连续体的性质不仅随着时间变化，而且随着观测点的位置变化，此时对时间求导则只能写成偏导数的形式。

如果我们希望让观测点以任意速度运动，则必须考虑观测点的运动对连续体性质的影响。 此时，我们引入物质导数： \(\def\d{\mathrm{d}} \def\D{\mathrm{D}} \begin{aligned} \frac{\mathrm D A(\vec x, t)}{\mathrm D t} &= \frac{\partial A(\vec x, t)}{\partial t} + \frac{\partial A(\vec x, t)}{\partial \vec x} \frac{\partial \vec x}{\partial t} \\ &= \frac{\partial A(\vec x, t)}{\partial t} + \vec v \cdot \nabla A \end{aligned}\) 这种视点称为人工欧拉-拉格朗日法。

物质导数可以视作是连接两种视点的桥梁。 只需要让其中的速度$\vec v$等于流体的速度$\vec U$，即可实现两者的转化。

流体力学的研究对象

流体力学是连续体力学的一部分，因此通常只在宏观尺度上处理问题。 欲满足宏观的连续性假设，物体分子的离散粒子性不能对欲求解的问题产生任何影响。 物体分子的离散性可由其平均自由程表示。 因此，流体力学通常只能解决特征尺度远大于该环境下分子的平均自由程的问题。 流体力学研究的物理量也通常都是宏观的物理量。

流体力学的研究对象通常是质点，或称流体微团。 对任意一个流体微团，我们假设其速度与流体的宏观速度总是相同。

流体微团的集合称为一个控制体，控制体可由其边界确定。

尺寸无穷小的控制体称为流体微粒。

流体微粒的无穷小尺寸允许我们将其物理性质视作均匀的，因此其速度、密度和任何物理量都可以视作仅仅与位置和时间相关。 因此，流体微粒的质量等于该点处的密度乘体积，而不需要进行积分。

流线与迹线

固定时间$t$下的流线（Streamlines）由以下方程给出： \(\vec U \times \mathrm{d} \vec x = 0\) 其中$\mathrm{d} \vec x$表示一条流线的切向量，$\vec U$表示流体的速度。

流体的迹线（Pathlines）表示某一粒子随时间运动的轨迹，由以下方程给出： \(\frac{\mathrm d \vec x}{\mathrm d t} = \vec U(\vec x, t)\)

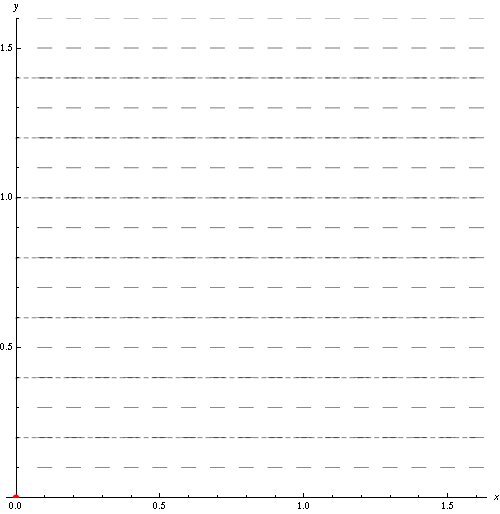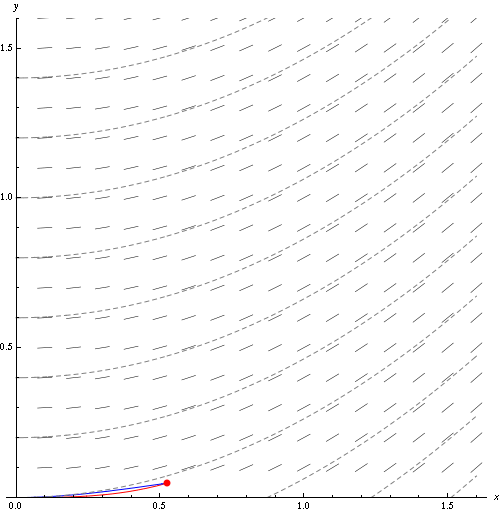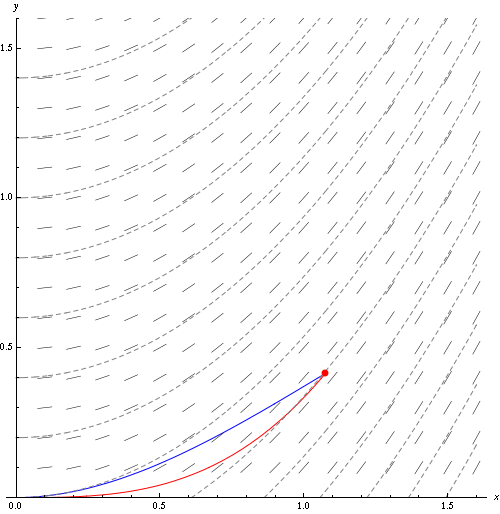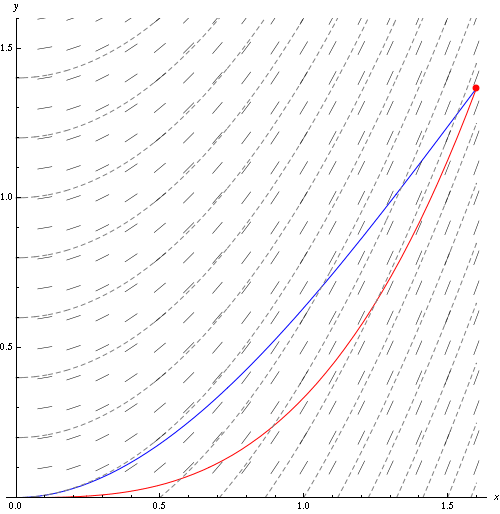
流线与迹线的定义比较相似，但两者并不相同。 上图中的灰色短线表示速度场，而灰色虚线表示流线。 红点的红色运动轨迹即为迹线。

当流体处于定常流动时，即流体的速度与时间无关时，流体的流线与迹线重合。

雷诺定理

雷诺定理给出了关于体积的积分量（如质量）对时间的导数关系。

设$S(t)$表示一控制体$D(t)$的边界，边界上一点的法向量为$\vec n$，边界一点的运动速度（非流体速度）为$\vec W$。 记$\varphi (\vec x, t)$为一物理量，$\varPhi(t)$为其在控制体上的积分： \(\varPhi(t) = \iiint_{D(t)} \varphi(\vec x, t) \mathrm d \nu\) 则： \(\frac{\mathrm d \varPhi(t)}{\mathrm d t} = \iiint_{D(t)} \frac{\partial \varphi}{\partial t} \mathrm d \nu + \iint_{S(t)} \varphi \vec W \cdot \vec n \mathrm d S\)

若控制体随流体一起运动，则$\vec W = \vec U$； 若控制体不动，则$\vec W = 0$。

雷诺定理可视为变限积分求导的莱布尼茨法则在三维上的推广。

不可压缩性

现在欲计算随流体运动的控制体的体积随时间的导数，令$\varphi = 1$，则$\varPhi = V$，代入雷诺定理，可得： \(\frac{\mathrm d V}{\mathrm d t} = \iint_S \vec U \cdot \vec n \mathrm d S = \iiint_{D} \nabla \cdot \vec U \mathrm d \nu\)

取体积微元$V = \nu$，可得： \(\frac{\mathrm d \nu}{\mathrm d t} = \nu \nabla \cdot \vec U\)

从而我们有以下命题：

一流体不可压缩，即微粒的体积不随时间变化，当且仅当 \(\nabla \cdot \vec U = 0\)

上文已经提出了一个证法，现在利用密度提出另一个证法。 流体不可压缩，即其微粒的密度不变： \(\frac{\mathrm d \rho}{\mathrm d t} = 0\) （此处为拉格朗日视点，注意区别欧拉视点的$\frac{\partial \rho}{\partial t} = 0$，后者只表示流动是定常的。） 从而： \(\frac{\mathrm d \rho}{\mathrm d t} = \frac{\partial \rho}{\partial t} + \vec v \nabla \rho = 0\) 由于流体的质量守恒，因此密度的变化率等于质量流出的速率，即： \(\frac{\partial \rho}{\partial t} = - \nabla (\rho \vec v)\) 从而： \(\begin{aligned} \vec v \nabla \rho - \nabla(\rho \vec v) &= 0 \\ v_i \partial_i \rho - \partial_i (\rho v_i) &= 0 \\ v_i \partial_i \rho - v_i \partial_i \rho - \rho \partial_i v_i &= 0 \\ -\rho \partial_i v_i &= 0 \\ - \rho \nabla \vec v &= 0 \end{aligned}\) 从而有$\nabla \vec v = 0$

质量方程

在流体力学中，和一般的物理学中一样，我们总是关心各种各样的守恒量，其中最重要的三个为质量、动量（或角动量）和能量。

本节中，我们将主要关心利用质量守恒给出流体的一些方程。

控制体的质量守恒

设控制体随流体一起运动，则有$\vec W = \vec U$，利用雷诺定理计算其质量：

\(\begin{aligned} \frac{\d M}{\mathrm d t} &= \frac{\mathrm d}{\mathrm d t} \iiint_D \rho \mathrm d v = 0\\ &= \iiint_D \frac{\partial \rho}{\partial t} \mathrm d t + \iint_S \rho \vec U \cdot \mathrm d \vec S \\ &= \iiint_D \frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \vec U) \d v = 0 \end{aligned}\) 从而我们得到了质量守恒的积分形式，两边取微分即可得到其微分形式。

现在将梯度算子拆开，然后注意到其中存在物质导数的形式，我们有： \(\frac{\mathrm D \rho}{\mathrm D t} + \rho \nabla \cdot \vec U = 0\) 对于不可压缩的流体，有： \(\frac{\mathrm D \rho}{\mathrm D t} = 0\)

随流体运动的控制体的密度满足： \(\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \vec U) = 0\) 或 \(\frac{\mathrm D \rho}{\mathrm D t} + \rho \nabla \cdot \vec U = 0\) 对不可压缩的流体，可写为： \(\frac{\mathrm D \rho}{\mathrm D t} = 0\)

改写雷诺定理

借助质量守恒方程，如果一个物理量可表示成与密度成正比的形式，即写成$\varphi = \rho \chi$的形式，那么其雷诺定理方程可以改写： \(\begin{aligned} \frac{\partial \rho \chi}{\partial t} &= \rho \frac{\partial \chi}{\partial t} + \chi \frac{\partial \rho}{\partial t} \\ &= \rho \frac{\partial \chi}{\partial t} - \chi \nabla \cdot (\rho \vec U) \\ &= \rho \frac{\partial \chi}{\partial t} + \rho \vec U \nabla \chi - \nabla \cdot (\rho \chi \vec U) \\ &= \rho \frac{\D \chi}{\D t} - \nabla \cdot (\rho \chi \vec U) \\ \implies \frac{\d}{\d t} \iiint \varphi \d v &= \iiint \frac{\partial \rho \chi}{\partial t} \d v + \iint \rho \chi \vec W \cdot \d \vec S \\ &= \iiint \rho \frac{\D \chi}{\D t} \d v + \iint \rho \chi (\vec W - \vec U) \cdot \d \vec S \end{aligned}\)

特别地，当$\vec W = \vec U$时，即控制体随流体运动时，有： \(\frac{\d}{\d t} \iiint \varphi \d v = \iiint \rho \frac{\D \chi}{\D t} \d v\)

控制体的受力

控制体上的受力可分为两个部分：表面力和体积力。

最常见的表面力为摩擦力和压力，这些力都和受力的面积的大小和方向有关。 这种力可以被表示为应力的形式。

最常见的体积力，也是流体力学中几乎唯一会常常出现的体积力，即物体的重力。 这种力作用于物体中的每一个微元上。

应力

本节中我们将主要研究流体中的应力。

根据前文的描述，我们知道，表面力的大小与方向和其所作用的表面密切相关。 我们希望研究表面力微元的大小和方向，这种情况下，应力可视为作用在单位面积上。 我们对表面力微元微分，此时有： \(\vec F_S = \iint_S \d \vec F_S = \iint_S T(\vec S) \d \vec S\) 我们尚且不知道$T(\vec S)$的物理和数学性质为何，只知道其一定是一个关于$\vec S$的函数。

根据对应力物理性质的研究，不难发现其关于面积法向量具有线性，因此我们可以考虑用矩阵（张量）来表述它。 注意到其将三维的面积法向量映射为三维的力向量，我们可以认为它是一个三维的方阵。 这正是柯西应力张量的定义。

柯西应力张量，简称应力，是一个二阶张量$\sigma$，满足： \(\sigma \cdot \vec S = \begin{pmatrix} \sigma_{11} & \sigma_{12} & \sigma_{13} \\ \sigma_{21} & \sigma_{22} & \sigma_{23} \\ \sigma_{31} & \sigma_{32} & \sigma_{33} \\ \end{pmatrix} \cdot \vec S = \vec F_S\) 即其将面积法向量映射为该面积元上的表面力向量。

若物体在各方向上均匀地承受沿法向向内的压力（比如浸没在水中的物体），则其应力张量为： \(\begin{pmatrix} -p & 0 & 0 \\ 0 & -p & 0 \\ 0 & 0 & -p \\ \end{pmatrix} = -p \mathbf{I}\) 这种应力称为纯压力。

流体应力的各向同性

流体所受应力的对角线上的三个元素（$\sigma_{11}, \sigma_{22}, \sigma_{33}$）相等。

这里涉及到一些结构力学的知识，因此不予证明。 形象的理解是，若对角线上元素不相等，则其一定承受剪力，而流体承受剪力意味着其一定发生不可逆的形变，而这是不可能的。

流体所受应力是一个对称矩阵。

我们利用角动量守恒证明该结论： \(\begin{aligned} \d \vec M &= \vec r \times (\sigma \cdot \vec n) \\ &= \epsilon_{ijk} r_j \sigma_{kl} n_l \\ \vec M &= \iint_S \vec r \times (\sigma \cdot \vec n) \d S \\ &= \iint_S \epsilon_{ijk} r_j \sigma_{kl} n_l \d S \\ &= \iiint_V \epsilon_{ijk} \frac{\partial r_j \sigma_{kl}}{\partial r_l} \d v & (\text{散度定理}) \\ &= \iiint_V \epsilon_{ijk} (\sigma_{kj} + r_j \frac{\partial \sigma_{kl}}{\partial r_l}) \d v & (\frac{\partial r_i}{\partial r_j} = \delta_{ij}) \\ &= \iiint_V \epsilon_{ijk} \sigma_{kj} \d v + \iiint \epsilon_{ijk} r_j \frac{\partial \sigma_{kl}}{\partial r_l} \d v \end{aligned}\) 我们尝试对这些项进行等价无穷小分析。 注意到对于无穷小的体积微元，$\sigma$及其导数可视为常数，有： \(\begin{aligned} \iiint \epsilon_{ijk} \sigma_{kj} \d v & \sim \iiint C \d v \sim V \\ \iiint \epsilon_{ijk} r_j \frac{\partial \sigma_{kl}}{\partial r_l} \d v & \sim \iiint C r_i \d v \sim V^{4/3} \end{aligned}\) 因此，$V \to 0$时，$\iiint \epsilon_{ijk} \sigma_{kj} \d v$是主项。 根据角动量守恒，对其我们有： \(\epsilon_{ijk} \sigma_{kj} = 0 \iff \sigma_{kj} = \sigma_{jk}\)

从而，我们得出以下定理：

流体的应力张量可写为： \(\sigma = - p \mathbf I + \tau\) 其中$\tau$是一个对角线为零的三维对称矩阵。

柯西定理

综合上文，我们可得出以下结论：

流体控制体所受的合力等于其上的表面力与其中的体积力之和： \(\vec F = \iint_S \sigma \cdot \d \vec S + \iiint_D \rho \vec f \d v\)

动量定理

我们已经求出了流体控制体的受力，因此我们可以直接对流体微粒应用牛顿第二定律，注意使用物质导数，因为此前的研究基于拉格朗日视点： \(\rho v \frac{\D \vec U}{\D t} = \vec F = \iint_S \sigma \cdot \d \vec S + \iiint_D \rho \vec f \d v\)

对表面力项应用散度定理： \(\begin{aligned} \rho v \frac{\D \vec U}{\D t} &= \iint_S \sigma \cdot \d \vec S + \iiint_D \rho \vec f \d v \\ &= \iiint_D \nabla \cdot \sigma + \rho \vec f \d v \end{aligned}\) 然后取微小体积$v$即可得流体的动量定理。

受表面力和体积力的流体的运动方程为： \(\rho \frac{\D \vec U}{\D t} = \nabla \cdot \sigma + \rho \vec f\) 其中$\sigma$是应力张量，其散度定义为¹： \((\nabla \cdot \sigma)_i = \partial_j \sigma_{ij}\) 向量的物质导数定义为： \(\left(\frac{\D \vec U}{\D t}\right)_i = \frac{\D U_i}{\D t}\)

这样我们就得到了流体力学最基本的两个等式： \(\left\{ \begin{aligned} & \frac{\D \rho}{\D t} + \rho \nabla \cdot \vec U = 0 \\ & \rho \frac{\D \vec U}{\D t} = \nabla \cdot \sigma + \rho \vec f \end{aligned} \right.\) 前者表示质量（密度）的变化，后者表示速度的变化，物质导数可展开为： \(\frac{\D}{\D t} = \frac{\partial}{\partial t} + \vec U \cdot \nabla = \frac{\partial}{\partial t} + U_1 \frac{\partial}{\partial x_1} + U_2 \frac{\partial}{\partial x_2} + U_3 \frac{\partial}{\partial x_3}\)

对动量方程应用改写的雷诺定理，令控制体固定，设$\chi = \vec U$，可得： \(\frac{\d}{\d t} \iiint_D \rho \vec U \d v = \iiint_D \rho \frac{\D \vec U}{\D t} \d v + \iint_S \rho \vec U \cdot \vec U \cdot \mathrm d \vec S\) 再将物质导数展开，可得动量方程的积分形式。

动量方程的积分形式为： \(\frac{\d}{\d t} \iiint_D \rho \vec U \d v = \iiint_D \rho \vec f \d v + \iint_S (\sigma + \rho \vec U \cdot \vec U) \d \vec S\)

1. 值得注意的是，该处定义与张量数乘的定义不同。考虑到$\sigma$是对称的，这两种定义对应力张量是等价的。一致的定义应为：\((\nabla \cdot \sigma)_i = \partial_j \sigma_{ji}\) ↩