时间相干性

在上一章中我们已经研究了在空间上具有一定尺寸的单色光源与点光源干涉的不同。 本章中我们将研究不同波长的光的干涉，即时间相干性。

准单色电磁波

准单色光源

我们首先研究准单色光源，即光源的光谱是一个宽度比较小的矩形的情形。

光谱与波数

任何一个现实的光源都不可能发出完美的单色光，即只有一个频率的电磁波。 然而，根据傅里叶变换的原理，光源发出的光总是具有连续的频谱，从而可以分解成无穷种单色光的积分： \(s(t) = \int_0^\infty a(f) \cos (2\pi f t + \varphi(f)) \mathrm d f\)

出于计算方便的考虑，我们使用波数$\sigma = \frac{1}{\lambda_0}$来描述光谱。 此时，光谱可以看作是谱密度关于波数的函数图像，其中谱密度的定义如下： \(\mathrm d \mathcal E(\sigma) = e_\sigma(\sigma) \mathrm d \sigma\) 满足： \(\mathcal E_0 = \int_0^\infty e_\sigma (\sigma) \mathrm d \sigma\)

值得注意的是，如果改用频率或波长求谱密度，其微元会发生变化，从而导致定义式不同。

准单色光源的矩形谱

我们使用矩形的谱，即一个门函数，来描述准单色光源的谱： \(e_\sigma (\sigma) = \begin{cases} e_0, & \sigma \in \left[ \sigma_m - \frac{\Delta \sigma}{2}, \sigma_m + \frac{\Delta \sigma}{2} \right] \\ 0, & \text{otherwise} \end{cases}\) 如果这个光源足以被称为准单色的，那么我们要求$\Delta \sigma \ll \delta_m$。

矩形谱的时间相干性

计算准单色光源的干涉情况： \(\begin{aligned} \mathcal E(M) &= \int_0^\infty 2 e_\sigma (\sigma) \mathrm d \sigma [1 + \cos (2\pi\sigma\delta(M))] \\ &= \int_{\sigma_m - \frac{\Delta\sigma}{2}}^{\sigma_m + \frac{\Delta\sigma}{2}} 2 e_0 \mathrm d \sigma [1 + \cos(2\pi\sigma\delta(M))] \\ &= 2 e_0 \Delta \sigma + 2 e_0 \left[ \frac{\sin 2\pi\sigma\delta(M)}{2\pi\delta(M)} \right]_{\sigma_m - \frac{\Delta\sigma}{2}}^{\sigma_m + \frac{\Delta\sigma}{2}} \\ &= 2 e_0 \Delta \sigma + \frac{2e_0}{2\pi\sigma(M)} [\sin(2\pi\left(\sigma_m+\frac{\Delta\sigma}{2}\right)\delta(M)) - \sin(2\pi\left(\sigma_m-\frac{\Delta\sigma}{2}\right)\delta(M))] \\ &= 2 e_0 \Delta\sigma + 2e_0 \Delta\sigma \cdot \mathrm{sinc}(\pi\Delta\sigma\delta(M)) \cos(2\pi\sigma_M\delta(M)) \end{aligned}\) 从而，我们可以发现，在高频（$\sigma_M$）的信号之上，还附加了一个低频的信号进行调制。 这样的话，其干涉的对比度之上还会出现一个辛格函数形成的包络线。

根据以上的研究，我们发现，在光程差为$\delta$的点附近，其对比度由一个辛格函数确定，这个对比度称为局部对比度： \(\Gamma_\text{局部}(\delta) = \frac{\mathcal E_{max} - \mathcal E_{min}}{\mathcal E_{max} + \mathcal E_{min}} = |\mathrm{sinc}(\pi \cdot \Delta\sigma \cdot \delta)|\)

这个对比度的形式和空间相干性的高度一致。 不同的是，这个对比度中的变量是光程差，而空间相干性中的是距离原点的光源的宽度。 这意味着在不改变仪器配置的情况下，可在同一干涉图样上发现时间相干性导致的对比度变化，而空间相干性导致的对比度变化只能通过调整仪器实现。

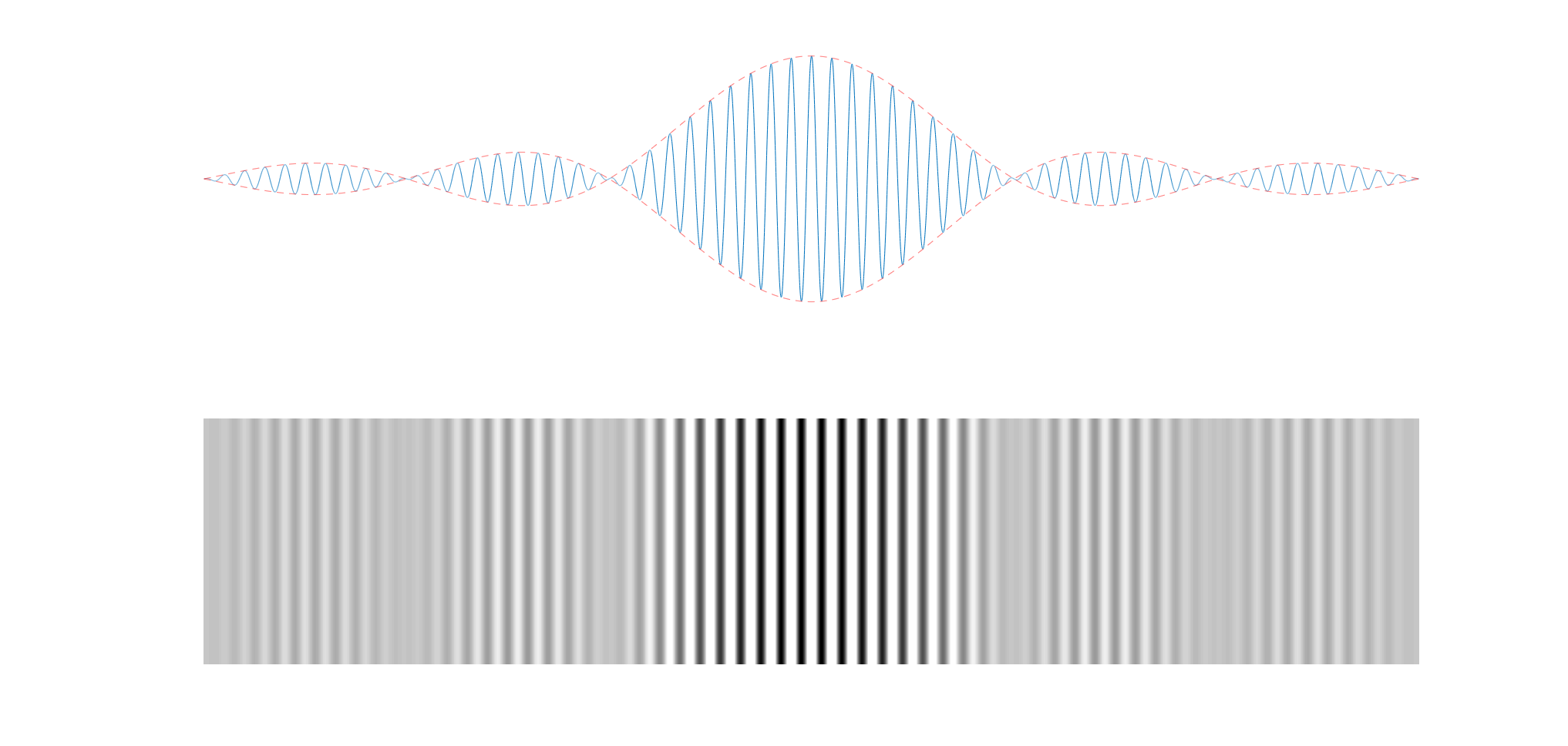
上图展示了光强、其包络线和衍射图样。

我们要求对比度较高以产生清晰的图案，因此我们要求光程差在零附近，且不宜超过辛格函数的第一个零点，从而： \(|\delta| < \frac{1}{\Delta \sigma}\)

显然，光谱越宽，达到这一要求就越困难。

更进一步地，设波长和波数谱的两个端点的下标为1和2，有： \(\begin{aligned} &\lambda_m = \frac{\lambda_1 + \lambda_2}{2} = \frac{\sigma_1 + \sigma_2}{2\sigma_1 \sigma_2} = \sigma_m \lambda_1 \lambda_2 \approx \sigma_m \lambda_m^2 \\ &\iff \lambda_m \approx \frac{1}{\sigma_m} \\ &\Delta\lambda = \lambda_2 - \lambda_1 = \frac{\sigma_1 - \sigma_2}{\sigma_2 \sigma_2} \approx \Delta\sigma \lambda_m^2 \\ &\iff \Delta \sigma = \frac{\Delta \lambda}{\lambda_m^2} \end{aligned}\) 从而我们要求：

对于矩形频谱的光源，若要使其条纹可见，需要满足： \(|\delta(M)| \le \frac{\lambda_m^2}{\Delta\lambda} = \mathcal l_c\) 其中$l_c$称为相干长度。

值得注意的是，相干时间和相干长度都是描述时间相干性，而非空间相干性的量。

双色光源

现在我们来研究一个特例：只有两根离散的谱线的光源。 钠灯就有这样两条相距不远的离散谱线，一根在570nm左右，另一根在590nm左右。

简单的计算给出： \(\mathcal E(M) = 2 e_0 [2 + 2 \cos(2\pi \sigma_M \delta(M)) \cos(\pi \Delta \sigma \delta(M))]\) 和上文一样，其干涉项由一个高频分量和一个低频分量组成，这个低频分量就是其包络线，也就是其对比度。

从而我们有： \(\Gamma = |\cos\pi \Delta \sigma \delta(M)| = | \cos \pi \frac{\Delta \lambda}{\lambda_m^2} \delta(M) |\)

对比度的零点位于$\delta(M) = \frac{\lambda_m^2}{\Delta \lambda}(n + \frac{1}{2})$处。 从而在对比度归零之前能够观察到的谱线条数满足： \(N\lambda_m = \delta(M_N) = \frac{\lambda_m^2}{\Delta\lambda} \iff N = \frac{\lambda_m}{\Delta\lambda}\)

对两条分立谱线的情况，设其平均波长为$\lambda_m$，差为$\Delta\lambda$，则其干涉图案随位置周期性出现并消失，且一个周期内含有： \(N = \frac{\lambda_m}{\Delta\lambda}\) 条谱线。

多色光干涉

本节中我们将研究白光的干涉。 白光的光谱通常可跨越400nm至800nm，且谱密度不等，因此不属于准单色光，更不属于单色光。 这种光源通常称为多色光。

根据之前的计算，光源的相干长度反比于谱的宽度。 对白光而言，其相干长度约为微米数量级，这意味着其干涉相当难以出现。

白光干涉的实验现象

我们通过迈克耳孙干涉仪可以观察到白光的干涉，此时我们规避了空间相干性的问题，其现象总结如下。

零级干涉条纹为白色。 在光程差满足小于相干长度的位置可以发现虹色，即发生色散现象。 在其他位置也可以观察到白色，但是这些白色的谱线出现缺级，即谱线中的一些部分出现缺失。

为了区别这两种白色，第一种白色可以称为亮白色。

其干涉条纹如下所示。

在肥皂泡或油膜上观察到的虹色就是这种干涉造成的。 具体而言，一层和外部介质不同的薄膜可以充当一面分光镜，对光线既起到反射的作用，又起到折射的作用。 当折射的光线遇到膜另一侧的介质时，又发生反射，从而发生分振幅干涉。 一般的肥皂泡的厚度仅有0.1微米至0.3微米¹，这就使得这两种光线的光程差小于相干长度，从而能够发生干涉。

1. Afanasyev, Yakov & Andrews, G Todd & Deacon, C.. (2011). Measuring soap bubble thickness with color matching. American Journal of Physics - AMER J PHYS. 79. 1079-1082. 10.1119/1.3596431. ↩