控制器设计

本章中我们将研究一些常见的控制器，最后以PID控制器作为控制理论的结尾。

控制器简述

对于一个系统，我们知道，其性能指标按照瞬态与稳态可分为阻尼与响应速度和稳定性与准确性（强健性）两组。 响应速度与准确性密切相关，阻尼和稳定性密切相关； 相应的，提高响应速度往往意味着降低阻尼和稳定性，而提高阻尼往往意味着降低速度与准确性。 系统的这些特点使得我们难以让一个系统同时让四种性能非常优秀。

为此，我们希望在控制系统中加入一个额外的环节，以此改善系统的性能。 这个环节就是控制器。

控制器的分类

常见的控制器可分为串联、并联和前馈三种。

串联控制器常出现在闭环系统计算误差之后，控制环节之前。 这种控制器是最常见的控制器，也是我们主要研究的控制器。

并联控制器也常出现在闭环系统中，但是其位于反馈环上，通过调节反馈的量来进行控制。

前馈控制器则通过将输入量“提前”传递给控制环节来起作用。 常见的前馈控制分为扰动补偿和误差补偿两种。

上图展示了常见的扰动补偿的控制器的一个例子。 设输入为$\phi(p)$计算其输出，可得： \(\begin{aligned} \epsilon(p) &= P(p) + H_2(p) [H_1(p) \phi(p) - C_p(p) P(p)] \\ &= H_1(p) H_2(p) \phi(p) + [1 - H_2(p) C_p(p)] P(p) \end{aligned}\) 若调整前馈控制器的传递函数，使得 \(1 - H_2(p) C_p(p) = 0 \iff C_p(p) = \frac{1}{H_2(p)}\) 那么输出就可以不受扰动的影响。 可惜的是，由于$H_2(p)$是一个因果系统，这意味着其分子多项式的阶数小于等于分母多项式的，从而取倒数后，$C_p$很有可能不是一个因果系统，从而不存在。 实践中我们要求两者约等于即可。

上图展示了一种常见的误差补偿控制器。 设输入为$X_c(p)$，计算器输出，计算其误差，可得： \(\begin{aligned} &\epsilon(p) = X_c(p) - H_3(p) H_2(p) [H_1(p) \epsilon(p) + C(p) X_c(p)] \\ \iff & [1 + H_1(p) H_2(p) H_3(p)] \epsilon(p) = [1 - H_2(p) H_3(p) C(p)] X_c(p) \end{aligned}\) 同理，若能满足 \(C(p) = \frac{1}{H_2(p) H_3(p)}\) 则能使得系统的误差与输入量无关。 然而由于因果系统的限制，我们也往往只能选择约等于的情况。

常见串联控制器

首先，对于常见的控制系统，添加一个串联控制器意味着在其开环传递函数上乘一个额外的传递函数。 我们主要关心开环传递函数，因为正如我们在前面几章中介绍的，闭环系统的性能可以从开环传递函数中简单地推出，而不用直接研究闭环传递函数。 我们设该控制器的传递函数为$C(p)$，则其频域响应为$C(j\omega)$。 那么，新的开环传函的增益和辐角可以写为： \(\left\{ \begin{aligned} G_{BO^\prime}(\omega) = 20 \lg |C(j\omega)| + 20 \lg |G_{BO} (\omega)| \\ \varphi_{BO^\prime}(\omega) = \arg C(j\omega) + \varphi_{BO} (\omega) \end{aligned} \right.\)

我们可以使用这个方式对添加控制器后的系统进行分析。

比例控制器

比例控制器是最常见最简单的控制器之一，其传递函数如下： \(C(p) = K, \; K \in \mathbb R_+\)

代入上式，不难发现其增益在$K>1$时增加，反之下降，而辐角不变。 从而，在波德图上，其增益部分随$K$值垂直平移，而辐角不变。

若$K>1$，从波德图上不难发现其裕度下降而带宽上升，从而稳定性下降而响应速度上升。 在尼柯尔斯图上观察，不难发现其曲线靠近临界点，从而阻尼下降。 注意到系统的稳态误差总是与整个系统的增益系数$K$反比，因此$K$上升会导致稳态误差下降，从而准确度上升。

若$K < 1$，那么结论都会反转。

上面做出的结论和章首的总结相符，因为从本质上讲乘一个常数并不会改变整个系统的结构性质。

微分控制器

最简单的微分控制器的传递函数如下： \(C(p) = Cp, \; C \in \mathbb R_+\) 然而，这个传递函数的分子次数大于分母次数，因此不是因果系统，所以不可能存在。 为此，我们需要进行改进。

滤波微分控制器

实际中使用的微分控制器具有以下传递函数： \(C(p) = \frac{Cp}{1 + \varepsilon p}\) 其中$\varepsilon$是一个远小于系统的特征时间的常量，从而$p$较小时其行为类似于一个微分器。

这个控制器是可以实现的，然而却存在一个巨大的问题。 不难发现这个控制器的截止频率为$\frac{1}{\varepsilon} \ge 1$。 输入频率远小于截止频率时，增益趋于负无穷；而输入频率非常高时，增益趋于常数。 这个控制器的行为和一个高通滤波器一致，因此得名。

然而，在控制器引入高通滤波并非非常实用，因为传感器的噪声往往是高频的，从而这个控制器会放大噪声，导致不良的后果。 因此，微分控制器往往不会单独使用。

比例微分控制器

比例微分控制器将一个微分控制器与一个比例控制器相加，在时域上可表示为： \(u(t) = A \epsilon(t) + B \dot \epsilon(t)\) 其中$\epsilon$表示误差，通常为控制器的输入。 那么，在频域上，其传递函数可写为： \(C(p) = A + B \frac{p}{1 + \varepsilon p} \approx \frac{1}{1+\varepsilon p}(A + Bp) = \frac{A}{1+\varepsilon p}(1 + \frac{B}{A} p)\) 注意到$\varepsilon$是一个非常小的数，因此可以进行这种近似。

在这个控制器中，我们依然使用滤波微分控制器作为微分控制器的近似。

计算其增益和辐角，可得： \(\begin{aligned} G_{dB-C} (\omega) &= 20 \lg A + 10 \lg (1 + \frac{B^2 \omega^2}{A^2}) - 10 \lg (1 + \varepsilon^2 \omega^2) \\ \varphi_C (\omega) &= \arctan \frac{B\omega}{A} - \arctan \varepsilon \omega \end{aligned}\)

这个控制器具有两个截止频率：$\omega_{c1} = \frac{A}{B}$和$\omega_{c2} = \frac{1}{\varepsilon}$。 考虑到$\varepsilon$非常小，这意味着$\omega_{c1} < \omega_{c2}$。

系统的波德图具有三条渐进线：

• $\omega < \omega_{c1}$时，增益为常数$20 \lg A$，相角为零；
• $\omega_{c1} < \omega < \omega_{c2}$时，增益为一条斜率为正二十的直线，相角为$\frac{\pi}{2}$；
• $\omega_{c2} < \omega$时，增益为常数$20 \lg \frac{B}{\varepsilon}$，相角为零。

这个控制器略好于直接的微分控制器，其不会完全抑制低频分量，但是仍会放大高频分量，导致噪音被放大。 因此，常见的控制器中一般不使用微分环节。 常见的PID控制器中通常只有20%含有微分环节。

相位超前控制器

相位超前控制器（Lead controller）可视作更一般的一种比例微分控制器。 注意到在PD控制器中，控制器的相角为正，这意味着控制器会使得信号的相角提前，这种控制器因此得名。 控制器的传递函数为： \(C(p) = K \frac{p + z_0}{p + p_0}, \quad |z_0| < |p_0|, K > 0\) 也可以写为： \(C(p) = A \frac{1 + a \tau p}{1 + \tau p}, \quad K > 0, \tau > 0, a > 1\) 和比例微分控制器不同，这里我们不再对参数的大小有要求。

我们可以计算其增益和辐角： \(\left\{ \begin{aligned} G_{dB-C}(j \omega) &= 20 \lg A + 10 \lg (1 + a^2 \tau^2 \omega^2) - 10 \lg(1 + \tau^2 \omega^2) \\ \varphi_C(j \omega) &= \arctan a\tau\omega - \arctan \tau\omega > 0 \end{aligned} \right.\)

系统的波德图具有三条渐进线：

• $\omega \le \frac{1}{a \tau}$时，增益为常数$20 \lg A$，相角为零；
• $\frac{1}{a \tau} < \omega \le \frac{1}{\tau}$时，增益为一条斜率为正二十的直线，相角为$\frac{\pi}{2}$；
• $\frac{1}{\tau} < \omega$时，增益为常数$20 \lg aA$，相角为零。

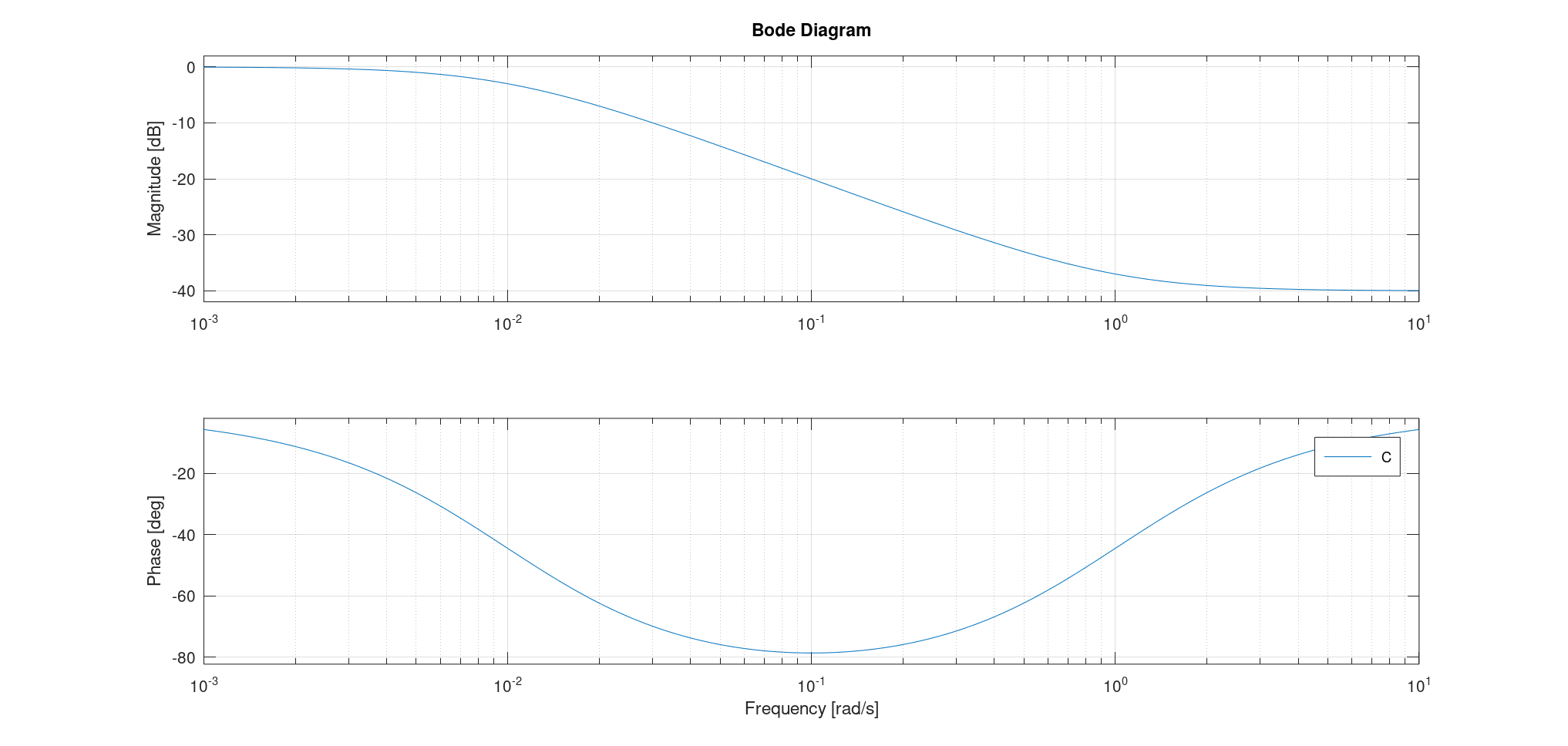
上图展示了一个典型的相位超前控制器的波德图，其中$A = 1, a = 100, \tau = 1$。

注意到相角似乎在两个截止频率的中点处取最大值，这个频率，以及该频率处对应的相角大小，是这种控制器的关键参数，因此我们希望求出它们。

---

我们考虑计算$\varphi_C$关于$\omega$的导数： \(\frac{\mathrm d \varphi_C}{\mathrm d \omega} = \frac{a \tau}{1 + a^2\tau^2\omega^2} - \frac{\tau}{1+\tau^2\omega^2} = 0\) 从而我们可以计算辐角取最大值时的角频率： \(\omega_m = \frac{1}{\tau \sqrt{a}}\) 注意到波德图为半对数图，因此这个点正好为两个截止频率的中点。

然后我们考虑计算这个角： \(\varphi_m = \varphi_c (\omega_m) = \arctan \sqrt{a} - \arctan \frac{1}{\sqrt{a}}\) 计算其正切和正弦，因为这些函数值更便于使用： \(\begin{aligned} \tan \varphi_m &= \frac{\sqrt{a} - \frac{1}{\sqrt{a}}}{1+1} = \frac{a-1}{2 \sqrt{a}} \\ \sin \varphi_m &= \frac{\tan \varphi_m}{\sqrt{1 + \tan^2 \varphi_m}} = \frac{a-1}{a+1} \end{aligned}\)

此外，注意到在此处控制器的增益为： \(G_{dB-C}(\varphi_m) = 10 \lg a\) 这一点在之后计算控制器的参数时会用到。

---

现在让我们来研究这个控制器对系统性能的影响。

• 稳定性：注意到系统的相角裕度为$\pi + \varphi_{BO}(\omega_{C0})$，若我们能够选择控制器使得其$\omega_m$恰好等于原开环函数的$\omega_{C0}$，那么系统的稳定性就能得到非常大的增强。这也为我们选择控制器的参数提供了一个思路。
• 阻尼：画出尼科尔斯图不难发现系统的图像远离了临界点，因此系统的阻尼增强。
• 准确性：该控制器和微分控制器一样会放大噪声，因此系统的准确性下降。
• 响应速度：被控制的系统的$\omega_c$向右移动，因此带宽增加，系统的响应速度上升。从另一方面看，系统放大了高频分量，因此响应速度上升。

---

最后我们考虑根据要求求解这个系统的参数。

1. 首先根据系统的准确性或响应速度的要求计算控制器的$A$，然后把这个增益乘到原开环传递函数上作为新的开环传递函数。
2. 使用计算新开环传递函数的稳定裕度。
3. 用要求的稳定裕度减去新开环传递函数的稳定裕度，即可得控制器的最大相角$\varphi_m$。实际应用中通常还需要再加上一些余量。
4. 利用$\sin \varphi_m = \frac{a-1}{a+1}$计算$a$。
5. 现在选择控制器的$\omega_m$，满足 \(G_{db-BO}(\omega_m) = -10 \lg a\) 我们知道控制器在$\omega_m$处的增益恰好为$10 \lg a$，因此加上控制器后，$\omega_m$即成为新的临界频率，这正是我们希望的。
6. 计算$\tau = \frac{1}{\omega_m \sqrt{a}}$。
7. 验证是否满足要求，若不满足则重新进行。

积分控制器

和微分控制器不同，积分环节本身就是因果性的，因此不必担心其是否能够存在这一问题。 我们知道，积分环节的传递函数为： \(C(p) = \frac{A}{p}\) 这个传递函数过于常见，因此我们不再仔细研究其性质，只是给出其对性能的影响。

• 稳定性：积分环节的相角为$- \frac{\pi}{2}$，因此系统的相角裕度下降，稳定性下降。
• 准确性：我们之前已经学习过，积分环节会让系统变得更加稳定。
• 阻尼：从尼柯尔斯图上可以发现系统接近临界点，因此阻尼下降。
• 响应速度：积分控制器通常会使响应速度下降，因为其滤去了高频分量。

比例积分控制器

将比例控制器和积分控制器组合在一起，即可获得比例积分控制器，其传递函数为： \(C(p) = A + \frac{B}{p} = \frac{Ap + B}{p}\)

这个系统通常会保持稳定性和阻尼不变，提高准确性并降低响应速度。

相位迟滞控制器

按照和相位超前控制器一样的思路，我们也可以利用比例积分控制器设计一个相位迟滞控制器，其传递函数为： \(C(p) = A \frac{1 + \tau p}{1 + a \tau p}, \quad A > 0, \tau > 0, a > 1\) 不难发现这个控制器与相位超前控制器高度对称。

以上是使用完全相同的参数绘制的相位迟滞控制器的波德图，注意现在$a$在分母的位置上。 由于传递函数相当于取了倒数，因此整个波德图被反转了。

按照完全相同的思路，我们不难发现其相角最大值在 \(\omega_m = \frac{1}{\tau \sqrt{a}}\) 处取得，和相位超前控制器完全一致。 然而，其相角是相反数，这就意味着： \(\sin \omega_m = \frac{1-a}{1+a}\)

相位迟滞控制器通常用来在提高增益的同时降低高频噪声的影响。 实际中，通常取$\omega_m \ll \omega_{C0}$，因此不会影响系统的稳定裕度。 同时取$A = a$，从而不会影响系统的临界频率。

比例积分微分控制器

通过将比例控制、积分控制和微分控制三个环节组合起来，可以同时获得这三种控制器的优点：

控制器类型	稳定性	准确性	响应速度	阻尼
比例控制（$K<1$）	+	-	-	+
比例控制（$K>1$）	-	+	+	-
积分控制	-	+++	-	-
微分控制	+	-	+	+

这种控制器的传递函数为： \(C(p) = A + \frac{B}{p} + \frac{Cp}{1+\epsilon p}\) 注意到因为因果系统的要求，微分控制环节不能直接使用求导的拉氏变换。

如果我们忽略微分环节的分母，那么这个系统的传递函数可以视为： \(C(p) = \frac{B}{p} (1 + \tau_1 p)(1 + \tau_2 p)\) 这种形式的传递函数更加利于分析。

超前迟滞控制器

超前迟滞控制器基本上就是两个控制器的组合，其传递函数为： \(C(p) = A \underbrace{\frac{1 + a \tau_1 p}{1 + \tau_1 p}}_{\text{超前部分}} \underbrace{\frac{1 + \tau_2 p}{1 + b\tau_2 p}}_{\text{迟滞部分}}\)

对超前部分，我们通常要求其最大相角的频率$\omega_{m}$和原系统开环传递函数的临界频率相近，而对迟滞部分我们通常要求其最小相角的频率远小于这个临界频率，这意味着控制器的四个重要频率之间满足： \(\frac{1}{b\tau_2} < \frac{1}{\tau_2} < \frac{1}{a\tau_1} < \frac{1}{\tau_1}\)

这个控制器的最大和最小相角满足： \(\sin \varphi_{min} = \frac{1-b}{1+b}, \; \sin \varphi_{max} = \frac{a-1}{a+1}\)

史密斯预测器

这一节中我们将主要研究如何控制一个带有迟滞环节的系统，根据拉普拉斯变换的平移性质，我们有： \(\mathcal L[f(t-\tau)] = e^{-\tau p} F(p)\) 这意味着一个带有迟滞环节的系统的传递函数具有一个额外的$e^{-\tau p}$乘数，正如下图所示。

当然，在控制器上乘上一个$e^{\tau p}$就可以完全抵消这个迟滞。 然而，显然，这种控制器不是因果的，因此不可能存在。 史密斯控制器通过引入一个额外的反馈环解决了这一问题。

这个系统的闭环传递函数为： \(\begin{aligned} \frac{X(p)}{X_c(p)} &= \frac{\frac{C(p)}{1+C(p)C^\prime(p)} H(p) e^{-\tau p}}{1 + \frac{K C(p)}{1 + C(p)C^\prime(p)} H(p) e^{-\tau p}} \\ &= \frac{C(p) H(p) e^{-\tau p}}{1 + C(p) [C^\prime(p) + K H(p) e^{-\tau p}]} \end{aligned}\)

现在，如果我们选择$C^\prime(p)$满足： \(C^\prime(p) = K H(p) [1 - e^{-\tau p}]\) 那么系统的传递函数就变为： \(\frac{X(p)}{X_c(p)}=\frac{1 + C(p) H(p)}{1 + K C(p) H(p)} e^{-\tau p}\) 这个传递函数相当于一个闭环系统的输出后面再附加了一个迟滞环节，从而将迟滞环节与系统隔离开来，不会对系统再产生任何不利影响。