光的衍射

本文中我们将研究光的衍射现象。

惠更斯-菲涅耳原理

惠更斯-菲涅尔原理由克里斯蒂安·惠更斯和奥古斯丁-让·菲涅尔共同提出，指出：“波前的每一点可以认为是产生球面次波的点波源，而以后任何时刻的波前则可看作是这些次波的包络”。 这些次波之间互相发生干涉，形成了衍射现象。

惠更斯原理的数学表述

设在笛卡尔坐标系中OXY平面上放置有一带有孔洞的不透光平面，其中的透光部分记为$\Sigma$。 在Z轴负半轴上某处存在一点光源$S$，发出波矢为$k_0$、振幅为$A_0$的单色光。 记$P$为平面上一点，点周围的面积元为$\mathrm d \sigma$。整个系统放置在折射率为$1$的均匀介质中。 惠更斯-菲涅尔原理说明，在光屏后任意一点的振幅为： \(\underline{A}(M) = K \iint_\Sigma \frac{A_0}{SP} \frac{1}{PM} e^{-i (k_0 \vec u) \cdot \vec{SP}} e^{-i (k_0 \vec{u^\prime}) \cdot \vec{PM}} \mathrm d \sigma(P)\) 其中$K$是一个常数。

和干涉一样，惠更斯原理对振幅而非光强求和。 我们将次波视作相干的。

首先计算从$S$出发到透光部分一点$P$的振幅，注意这个波是球面波： \(\underline A_s (p) = \frac{A_0}{SP} e^{-i(k_0 \vec u) \cdot \vec{SP}}\) 然后考虑次波，注意微元符号： \(\mathrm d \underline A_p (M) = \frac{K A_s}{PM} e^{-i (k_0 \vec u^\prime) \cdot \vec{PM}} \mathrm d \sigma(P)\) 从而： \(\begin{aligned} A(M) &= \iint_\Sigma \mathrm d A_p (M) \\ &= K \iint_\Sigma \frac{A_0}{SP \cdot PM} e^{-i(k_0 \vec u) \cdot \vec{SP}} e^{-i(k_0 \vec u^\prime) \cdot \vec{PM}} \mathrm d \sigma(P) \end{aligned}\)

亥姆霍次衍射理论说明常数$K = \frac{i}{\lambda}$，此处不对此加以证明。

衍射的不同类型

为了区分不同的衍射类型，我们定义菲涅耳数： \(\mathcal F = \frac{a^2}{L \lambda}\) 其中$a$表示产生衍射的物体的特征大小，比如圆孔的半径； $L$表示观察衍射的光屏距离衍射物体的距离； $\lambda$表示光的波长。
$F \gg 1$时，认为不发生衍射； $F \approx 1$时，认为发生近场衍射，又称菲涅尔衍射； $F \ll 1$时，认为发生远场衍射，又称夫琅禾费衍射。

我们只研究夫琅禾费衍射。

对于远场的情形，我们可以使用凸透镜来将平行光聚焦在光屏上。 由于成像的是平行光，这相当于光屏距离物体无穷远。 因此通常来说，当系统具有一定的光学能力（如含有平面镜或透镜时），我们主要研究夫琅禾费衍射，否则研究菲涅尔衍射。

夫琅禾费衍射

夫琅禾费衍射的数学表述

考虑一位于无穷远处的波长为$\lambda$的单色平行光源，观测图样的光屏位于无穷远处。 设向量： \(\vec u = \begin{pmatrix} \alpha \\ \beta \\ \gamma \end{pmatrix}, \; \vec u^\prime = \begin{pmatrix} \alpha^\prime \\ \beta^\prime \\ \gamma^\prime \end{pmatrix}\) 为二分别表示入射光和衍射光方向的单位向量。 设$P(X,Y)$为光屏上一点，则根据惠更斯原理，衍射光的复振幅为： \(\underline{A}(M) = K^\prime A_0 \iint_\Sigma \exp \left[i \frac{2\pi}{\lambda} \Big((\alpha^\prime - \alpha)X + (\beta^\prime - \beta)Y\Big) \right] \mathrm d X \mathrm d Y\)

直接代入原方程，注意球面波变为平面波，因此波的振幅和距离无关： \(\begin{aligned} A(M) &= K A_0 \iint_\Sigma e^{-i(k_0 \vec u) \cdot \vec{SP}} e^{-i(k_0 \vec u^\prime) \cdot \vec{PM}} \mathrm d \sigma(P) \\ &= K A_0 \iint_\Sigma e^{-i(k_0 \vec u) \cdot (\vec{OP}-\vec{OS})} e^{-i(k_0 \vec u^\prime) \cdot (\vec{OM} - \vec{OP})} \mathrm d \sigma(P) \\ &= K A_0 e^{ik_0 \vec u \cdot \vec{OS}} e^{-ik_0 \vec u^\prime \vec{OM}} \iint_\Sigma e^{ik_0 \vec{OP} \cdot (\vec u^\prime - \vec u)} \mathrm d X \mathrm d Y \\ &= K^{\prime} A_0 \iint_\Sigma e^{i k_0 ((\alpha^\prime - \alpha)X + (\beta^\prime - \beta)Y)} \mathrm d X \mathrm d Y \end{aligned}\)

大多数时候，光线是正入射的，此时$\vec u = (0,0,1)$，方程变为： \(A(M) = K^\prime A_0 \iint_\Sigma e^{i \frac{2\pi}{\lambda}(\alpha^\prime X + \beta^\prime Y)} \mathrm d X \mathrm d Y\)

夫琅禾费衍射实验

夫琅禾费衍射试验非常容易设计实现。

为了产生一束平行光，我们需要把光源放置在一面凸透镜的焦点处，这可以由自准直法实现。 同理，为了将衍射图样成像在无穷远处，我们在光屏之前放置一个凸透镜，然后使其聚焦在光屏上。

除此之外，我们还要求衍射物尺寸尽量小于波长，以此满足菲涅耳数无穷小。

设光屏前使用的凸透镜焦距为$f^\prime$，则光屏上一点$(x,y,z)$处的复振幅为： \(A(M) = K^\prime A_0 \iint_\Sigma e^{i \frac{2\pi}{\lambda}(\frac{x}{f^\prime}X + \frac{y}{f^\prime}Y)} \mathrm d X \mathrm d Y\)

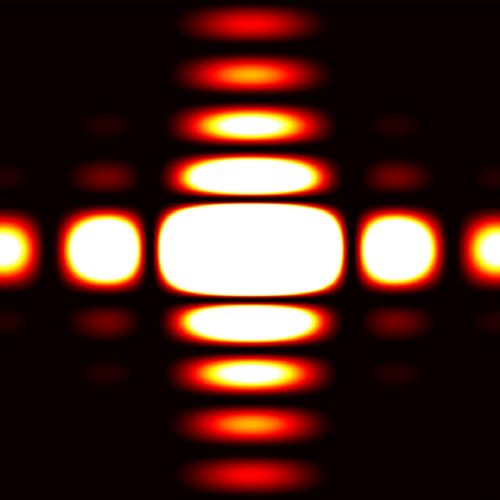
矩形孔

现在，我们假设光屏铅垂方向为Y轴，水平方向为X轴，矩形孔的高度，即Y轴长度，为$L$，宽度为$l$，那么矩形孔衍射图案的光强为： \(\mathcal E(x,y,z^\prime) = \mathcal E^\prime \mathrm{sinc}^2 \left( \frac{\pi l x}{\lambda f^\prime} \right) \mathrm{sinc}^2 \left( \frac{\pi L y}{\lambda f^\prime} \right)\)

根据辛格函数的性质，衍射图样最中央亮斑的大小，即距原点最接近的两个零点的距离，在Y轴上是$\frac{2\lambda f^\prime}{L}$，在X轴上是$\frac{2\lambda f^\prime}{l}$。

下面是矩形孔的衍射图样，注意若孔在竖直方向上比水平方向上大五倍，那么其在竖直方向上的亮纹长度只有水平方向的五分之一。

透射系数

我们使用透射系数定量地研究衍射物的性质。

设$E$为光屏上一点，而$E_-$、$E_+$分别为光入射和出射方向上在$E$点附近无穷近两点，则该点处的透射系数（也称透明度）$\underline{t}$定义为满足下一等式的复数： \(\underline{t}(E) \cdot \underline{A}(E_-) = \underline{A}(E_+)\)

透射系数的模长表示了光透过衍射物的程度，而辐角表征了相位的变换。 为了简化问题，我们通常只研究其等于实数零或一两种情况。

我们通常使用以下这个近似： \(\underline{t}(P) = \frac{\underline{A}_{\text{存在衍射物}}(P)}{\underline{A}_{\text{不存在衍射物}}(P)}\) 这意味着我们假设光线是从法向入射的，且忽略所有折射的光线。

若透射系数的模长等于零，那么我们称其在此处是不透明（Opaque）的；如果透射系数的模长等于一，那么我们称其为透明（Transparent）的；如果透射系数介于两者之间，则称其为部分吸光的。

衍射与傅里叶变换

不难注意到在夫琅禾费衍射的公式中，存在非常类似傅里叶逆变换的结构。 实际上，我们有以下命题成立：

在夫琅禾费衍射的情况下，出射光的复振幅为衍射物的透射系数的傅里叶逆变换： \(\underline{A}(x,y,z) = K^\prime A_0 \mathcal F^{-1}[t_\Delta(X,Y)](\frac{\alpha^\prime - \alpha}{\lambda}, \frac{\beta^\prime - \beta}{\lambda})\)

这里我们忽略傅里叶变换的归一化问题，使用最简单的定义： \(\mathcal F[f](u) = \int_{-\infty}^{+\infty} f(r) e^{-2i\pi u r}\mathrm d r, \mathcal F^{-1}[F](r) = \int_{-\infty}^{+\infty} F(u) e^{2i \pi u r} \mathrm d u\)

互补图案的衍射

如果两个衍射物体$\Delta, \Delta^\prime$满足： \(\forall P, \; \underline{t}_{\Delta}(P) = \underline{t}_{\Delta^\prime}(P) = 1\) 那么称这两个物体是互补的。

巴比涅原理指出，互补图案的衍射图样完全一致。

（巴比涅原理）两个互补的衍射物产生的衍射图样的形状完全一致，且其复振幅之和等于未加任何衍射物时光线产生的复振幅。

\(\begin{aligned} \underline{A}_\Delta(M) &= K^\prime A_0 \mathcal F^{-1}[\underline{t}_\Delta](\frac{\alpha^\prime - \alpha}{\lambda}, \frac{\beta^\prime - \beta}{\lambda}) \\ &= K^\prime A_0 \mathcal F^{-1}[1 - \underline{t}_{\Delta^\prime}](\frac{\alpha^\prime - \alpha}{\lambda}, \frac{\beta^\prime - \beta}{\lambda}) \\ &= K^\prime A_0 (\delta(\frac{\alpha^\prime-\alpha}{\lambda}) \delta(\frac{\beta^\prime-\beta}{\lambda}) - \mathcal F^{-1}[\underline{t}_{\Delta^\prime}](\frac{\alpha^\prime - \alpha}{\lambda}, \frac{\beta^\prime - \beta}{\lambda})) \end{aligned}\) 如果忽略其中的狄拉克δ函数，即可得证。

衍射图样的位移与缩放

沿OXY平面平移衍射物，其衍射图案不发生变化； 若将衍射物在X轴和Y轴上分别加上系数为$\alpha_X, \alpha_Y$的缩放，则衍射图案在两轴上分别发生系数为$\frac{1}{\alpha_X}$和$\frac{1}{\alpha_Y}$的缩放，且复振幅的模长变为$\alpha_X \cdot \alpha_Y$倍。

这两条定理可以非常容易地用傅里叶变换的性质验证。

衍射的几个例子

矩形图案

矩形衍射物的夫琅禾费衍射具有以下特点：

1. 其光强满足： \(\mathcal E(M) = \mathcal E_0 \mathrm{sinc}^2\left( \frac{\pi l x}{\lambda f^\prime}\right) \mathrm{sinc}^2 \left( \frac{\pi L y}{\lambda f^\prime} \right)\) 其中$l,L$分别为矩形窗口的X轴和Y轴大小。
2. 光强最大值位于屏幕中心，即光源投影所在的位置，与衍射物无关。
3. 亮度在 \(x = n \frac{\lambda f^\prime}{l}, y = n \frac{\lambda f^\prime}{L}\) 处为零。
4. 中心亮斑约具有84%的能量。
5. 亮斑的大小反比于衍射物的大小。

当其Y轴长度远大于X轴长度时，可见条纹状的衍射图样，此时退化为与衍射光栅相同。

环形图案

若衍射物为一半径为$R$的圆盘，则其衍射图样为圆环，称为艾里斑。 其光照强度为： \(\mathcal E(M) = \mathcal E_0 \left( \frac{2 J_1(\theta)}{\theta} \right), \; \theta = \frac{2\pi\rho R}{\lambda f^\prime}, \; \rho = \sqrt{x^2 + y^2}\)

其中$J_1$为一类贝塞尔函数。

研究表明，艾里斑的中心亮斑的半径约为： \(\rho_{\text{Airy}} = 0.610 \frac{\lambda f^\prime}{R}\) 正如预料到的，其大小与衍射物的大小成反比。

瑞利判据

如果观察远处的两个非常接近的物体，那么其像之间很可能发生干涉，瑞利判据给出了定量判定两个物体是否仍然可以分辨的方法。

两个相等强度的点光源，在考虑到其衍射的情况下，若其中一个的中央极大值，刚好落在另一个的第一极小值，则称它们刚好能够分辨。 若它们的距离再远一点，就是能够分辨；再近一点，则无法分辨。