晶格动力学

本文研究晶格的动力学，即晶格中原子的运动。 在之前的模型中，我们总是假设晶格中的原子是静止的；然而，这与 X 射线衍射给出的结果不相符——X 射线衍射的结果说明其中的原子总是在振动的。

在研究固体物理时，我们通常使用波恩-冯·卡门边界条件，此时要注意晶体中的两种平移周期性： \(\mathbf u(x_j, t) = \mathbf u(x_j + L, t) = \mathbf u(x_j + N a, t),\) 其中$L$是整个材料的大小，而$a$是晶格的大小，$N$是整个材料中的晶格数，此处假设材料为一维，多维的情况是容易推广的。 根据傅里叶变换，有 \(\mathbf u(x_j, t) = \sum_q A_{q, j} \exp[iqx_j], \, q = n\frac{2\pi}{L} = n\frac{2\pi}{Na}.\) 注意到$a$的傅里叶变换即在倒易空间中，因此$L$的傅里叶变换$q$也在倒易空间中，$q$也称为格波。 格波作为傅里叶变换的基底，具有正交归一性，即 \(\int_{-L/2}^{L/2} \exp[iqx] \exp[iq'x] \,\mathrm d x = L\delta_{q, q'}\)

由于$q$由材料的周期性和晶格的周期性同时组成，我们可将其写为两者之和 \(\begin{multline} q = n_L \frac{2\pi}{L} + n_a \frac{2\pi}{a} \implies \\ \mathbf u(x_j, t) = \sum_{k \in \text{布里渊区}} \sum_{G \in \text{倒空间}} A_{k+G, j} \exp[i(k+G)x_j]. \end{multline}\) 重组可得 \(\begin{aligned} \mathbf u(x_j, t) &= \sum_k \exp[ikx_j] \sum_G A_{k+G, j} \exp[iGx_j] \\ &= \sum_{k \in \text{布里渊区}} \exp[ikx_j] v_{k,j}(x_j), \end{aligned}\) 其中$v_{k,j}$是一个周期为$a$的周期函数。

根据 \(q = n\frac{2\pi}{L} = n\frac{2\pi}{Na}\) 的关系，一维材料中由多少个原胞，那么第一布里渊区中就有多少个$q$点。 实际情况中，$N$会极其大，进行模拟时会从较小的值迭代增加，直到收敛。

经典晶格动力学

波恩-奥本海默近似

波恩-奥本海默近似(Born-Oppenheimer Approximation)认为，由于电子的质量远小于原子核，因此电子只在视为静止原子核产生的势场中运动，而原子核则只受到电子的平均作用力。 更进一步地，可将这种势场归纳于一般的弹簧产生的弹性势能的势场中。

在原子$n$的平衡位置$u_n$，根据级数展开，其势能满足 \(\begin{multline} W = \sum_{j,n} \sum_{a=1}^3 W_{j,n} + \sum_{j,n} \sum_{a=1}^3 \frac{\partial W}{\partial {u_{a,j}}} u_{a,j}\\ + \sum_{j,n} \sum_{a,b=1}^3 \frac{\partial^2 W}{\partial u_{a,j} \partial u_{b,j}} u_{a,j} u_{b, j} + O(u^3), \end{multline}\) 势能的一阶导数等于零，我们取二阶导数进行近似，得到类似弹簧弹性势能的表示，从而 \(m \ddot u_n = - 2 \sum_n V_{n,j} (u_j - u_n),\) 其中$V_{n,j}$表示两原子之间作用产生的势能的二阶小量的一阶导。 将$u_n$的谐波解代入，可将方程重组为矩阵的形式， \(-\omega_q^2 A_j(q) + \sum_n D_{n,j} A_n(q) = 0, \implies \hat D \vec A(q) = \omega^2_q \vec A(q).\)

一维单原子链

我们现假设存在一条两种原子交错组成的链条，第一种原子与平衡位置的距离记为$x_i$，第二种原子的距离记为$y_i$，两种原子之间以弹性系数不同（$K_S, K_L$）的弹簧相连，则微分方程为 \(\left\{ \begin{aligned} m \ddot x_i &= - K_S (x_i - y_i) - K_L(x_i - y_{i-1})\\ m \ddot y_i &= - K_S (y_i - x_i) - K_L(y_i - x_{i+1}) \end{aligned} \right..\)

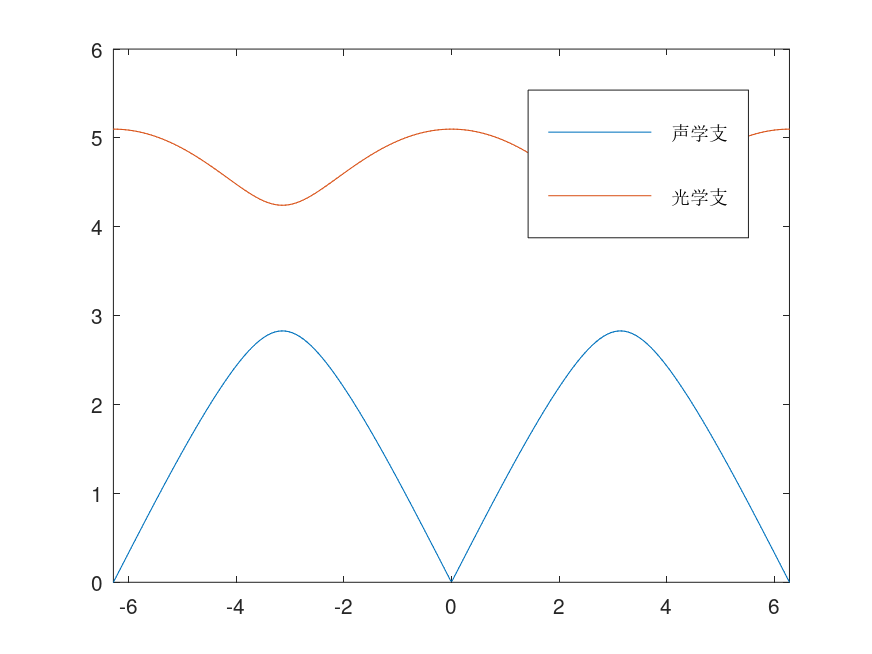
带入谐波解，得到矩阵形式 \(\begin{pmatrix} \Omega_S^2 + \Omega_L^2 & -(\Omega_S^2 + \Omega_L^2 e^{-iqa}) e^{iqd} \\ -(\Omega_S^2 + \Omega_L^2 e^{iqa}) e^{-iqd} & \Omega_S^2 + \Omega_L^2 \end{pmatrix} \begin{pmatrix} X \\ Y \end{pmatrix} = \omega_q^2 \begin{pmatrix} X \\ Y \end{pmatrix}.\) 求解该特征值问题，得到 \(\omega_q = \sqrt{\Omega_S^2 + \Omega_L^2 \pm \sqrt{\Omega_S^4 + \Omega_L^4 + 2 \Omega_S^2 \Omega_L^2 \cos qa}}.\) 这两个特征值对应的色散关系，根据$q$趋于零时的行为，分别称为声学支和光学支：

• 若$q \to 0$时，$\omega_q \to 0$，则称为声学支，此时原子同向振动，该色散关系类似于声波等物质波；
• 否则，称为光学支，此时原子反向振动，该色散关系类似于电磁波。

格波的量子化

考虑到晶格的振动是简谐波，利用湮灭和产生算符，格波的能量可进行量子化： \(\hat H = \sum_q (\hat{a}^\dagger \hat a + \frac 1 2) \hbar \omega(q),\) 其中$\hat a$是湮灭算符，$\hat{a}^\dagger \hat a$即为粒子数算符$\hat N$。 这种量子称为声子 (Phonons)。 从而本征态$s$的能量为 \(\epsilon_s = \sum_q (n_{q,s} + \frac 1 2) \hbar \omega(q),\) 而其特征向量可由每个模态的例子数量$n_{q,s}$表出 \(\left| \phi \right> = \left| n_1, n_2, \dots \right>.\) 固体中总的模态数等于自由度数，在整个固体中模态数可视为无穷大。

计算热容

我们现在可利用正则系综来计算声子系统的热容，首先计算正则配分函数： \(\begin{aligned} Z &= \sum_s \exp \left[ -\beta \sum_q (n_{q,s} + \frac{1}{2}) \hbar \omega(q) \right] \\ &= \exp \left[-\frac{\beta}{2} \sum_q \hbar \omega(q)\right] \sum_s \exp\left[-\beta \sum_q n_{q,s} \hbar \omega(q)\right] \\ &= \exp \left[-\frac{\beta}{2} \sum_q \hbar \omega(q)\right] \sum_s \prod_q \exp \left[ -\beta n \hbar \omega(q) \right] \\ &= \exp \left[-\frac{\beta}{2} \sum_q \hbar \omega(q)\right] \prod_q \sum_{n = 0}^{\infty} \exp \left[ -\beta n \hbar \omega(q) \right], \end{aligned}\) 最后一步颠倒了求和顺序，将对每个状态$s$的每个模式$q$求和变为对每个模式$q$的声子数$n$求和。 从而利用无穷级数求和 \(Z = \exp \left[-\frac{\beta}{2} \sum_q \hbar \omega(q)\right] \prod_q \frac{1}{1-\exp[-\beta\hbar\omega(q)]}.\) 可注意到此处出现了玻色-爱因斯坦分布，这是自然的，因为声子是玻色子。

内能为 \(U = - \frac{\partial \ln Z}{\partial \beta} = \sum_q \left(\frac{1}{\exp[\beta\hbar\omega(q)]-1} + \frac{1}{2} \right) \hbar \omega(q).\) 现在记 \(\overline{n_q} = \frac{1}{\exp[\beta\hbar\omega(q)]-1}\) 表示平均粒子数，从而单位体积的热容为 \(C_V = \frac{1}{V} \frac{\partial}{\partial T} U = \frac{1}{V} \sum_q \hbar \omega(q) \frac{\partial}{\partial T} \overline{n_q}.\)

直接求和过于复杂，我们考虑进行两种近似：高温近似与低温近似。

高温与低温近似

在最开始，我们利用能量近似定理对固体的摩尔比热进行过近似： \(C_V = \frac{\partial}{\partial T}\left(\underbrace{\frac{3}{2} k T}_\text{Kinetic} + \underbrace{\frac{3}{2} kT}_\text{Potential} \right) N_A = 3R.\) 在高温情况（热力学极限）下，我们期望声子给出的结果与经典近似相同。

在高温下，我们认为 \(kT \gg \hbar \omega(q) \iff \beta \hbar \omega(q) \ll 1,\) 从而可对$\overline{n_q}$进行级数展开： \(\overline{n_q} = \frac{1}{\exp[\beta \hbar \omega(q)] - 1} \approx \frac{1}{\beta\hbar\omega(q)} = \frac{k T}{\hbar \omega(q)}.\) 因此 \(C_V = \frac{1}{V} \sum_q k.\) 注意到模式数与自由度个数一致，若考虑单个原子共有三自由度，则体积比热为 \(C_V = \frac{3k}{V} N.\) 其中$N$是固体所含的原子数。

在低温下，我们认为$\omega \to 0$，从而仅考虑色散关系中的声学支，且可将色散关系视为是线性的。 考虑到较大的固体内$q$的取值稠密，我们可将离散的求和视为积分： \(C_V = \frac{1}{V} \frac{\partial}{\partial T} \sum_\alpha \int_\Omega \frac{\hbar \omega(q)}{\exp[\beta\hbar\omega(q)] - 1} \frac{V}{(2\pi)^3} \, \mathrm d \Omega q^2 \,\mathrm d q,\) 其中$\alpha$表示对所有声学支求和，$\Omega$是在三维空间中的积分，一般视为一个球。 现在将色散关系视为线性，令 \(\omega_\alpha \approx c_\alpha q \implies y = \beta \hbar c_\alpha q,\) 从而 \(C_V = \frac{1}{(2\pi)^3} \frac{\partial}{\partial T} \frac{(kT)^4}{\hbar^3} \sum_\alpha \int_\Omega \frac{\mathrm d \Omega_q}{c_\alpha^3} \int_{-\infty}^{\infty} \frac{y^3}{e^y - 1} \, \mathrm d y.\) 最后一个积分的解为 \(\int_{-\infty}^{\infty} \frac{y^3}{e^y - 1} \, \mathrm d y = \frac{\pi^4}{15}.\) 现在令 \(\frac{1}{\overline c^3} = \frac{1}{3} \sum_\alpha \int \frac{\mathrm d \Omega_q}{4\pi c_\alpha^3}\) 称为平均声速，则体积比热为 \(C_V \approx \frac{2\pi^2}{5} k \left( \frac{kT}{\hbar \overline c} \right)^3,\) 这与实验测定的绝缘体的低温比热符合。

中间温度近似

对于中间温度情况，常见的近似是爱因斯坦近似，此时只考虑光学支，且将其色散关系视为常数，即 \(\omega(q) = \omega_E.\) 对声学支，则有德拜近似，此时仍将色散关系视为线性，但需要降低模式数以避免过高的$q$值。