线性时不变一阶与二阶系统
我们来考虑几个典型系统。
积分系统
积分系统的传递函数为: \(H(p) = \frac{K}{p}\) 从而。有: \(H(j \omega ) = -j \frac{K}{\omega} \implies \left\{ \begin{aligned} G_{db} ( \omega ) &= 20 \log K - 20 \log \omega \\ \phi ( \omega ) &= - \frac{\pi}{2} \end{aligned} \right.\)
要点:
- 波德图增益部分为一根斜率为-20的直线,辐角始终为$- \frac{\pi}{2}$;
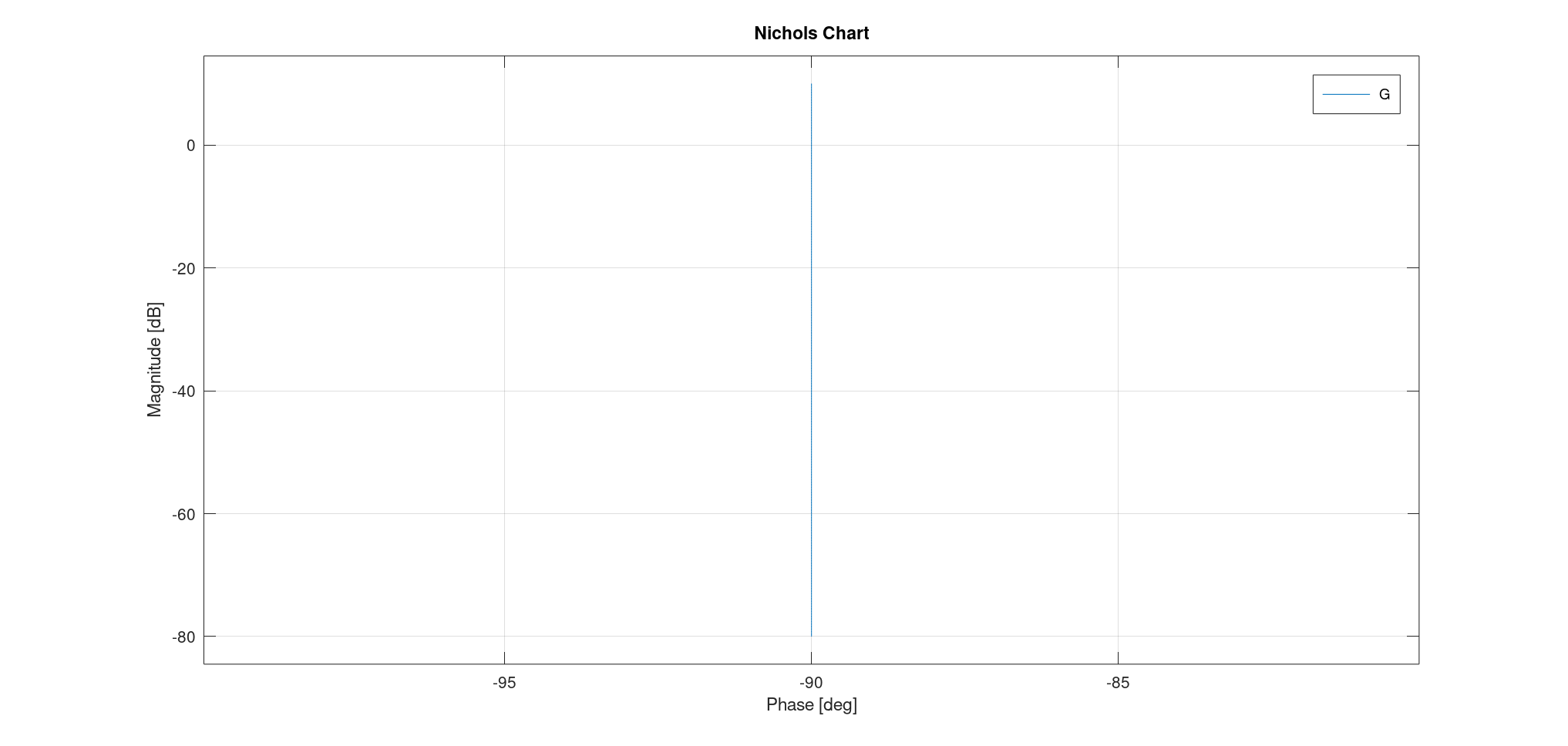
- 尼柯尔斯图为一根直线,随$\omega$增大从$(0, +\infty)$变为$(0,-\infty)$
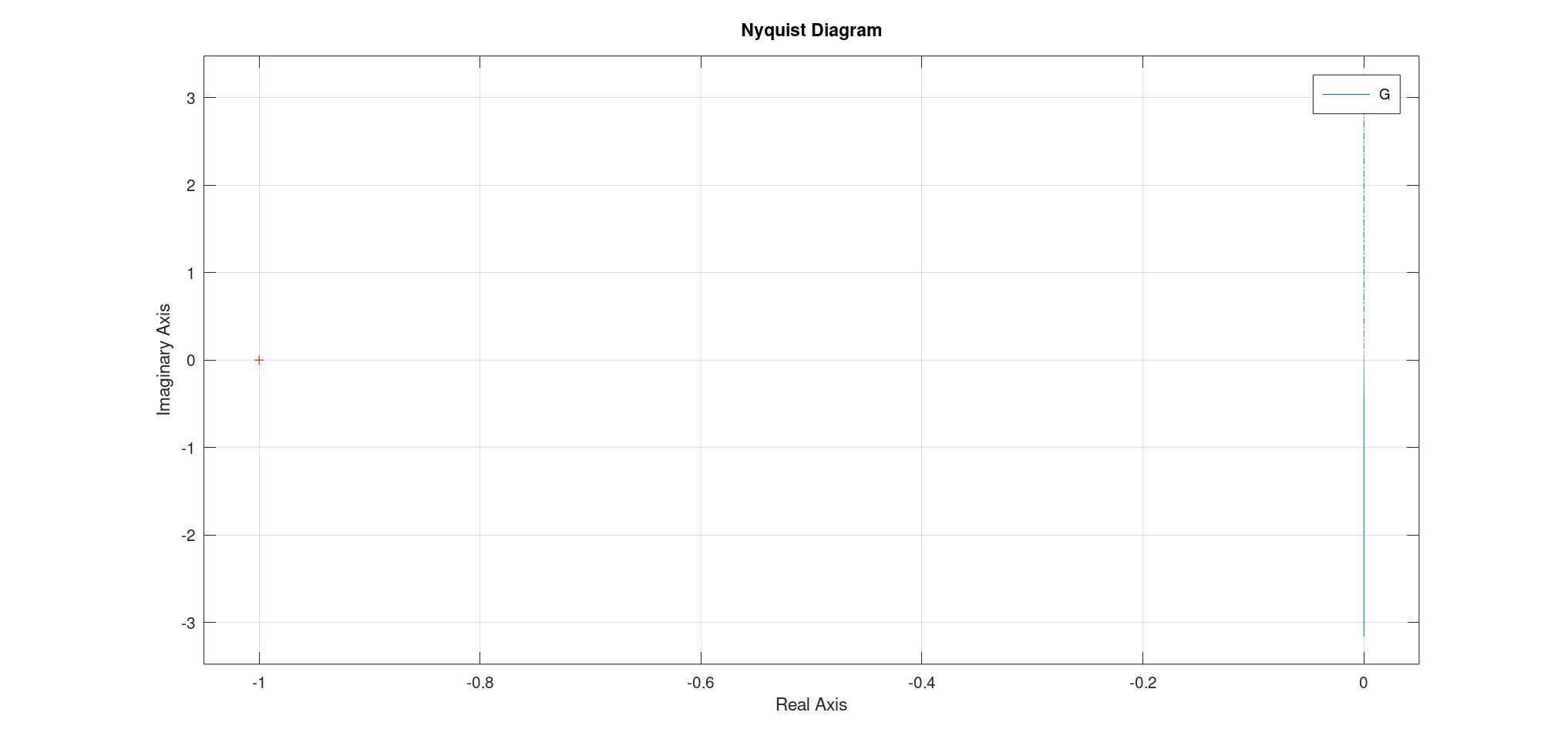
- 奈奎斯特图为一根直线,随$\omega$增大从$(0, -\infty)$变为$(0,0)$。

一阶系统
一阶系统的传递函数为: \(H(p) = \frac{K}{1 + \tau p}\)
时域响应
冲激响应
考虑冲激函数$e(t) = A \delta (t) \iff E(p) = A$ 则其响应为$S(p) = \frac{KA}{1 + \tau \pi} \iff s(t) = \frac{KA}{\tau} e^{-\frac{t}{\tau}} u(t)$ 从而其冲激响应为一从$(0, \frac{KA}{\tau})$开始的指数衰减函数,特征时间为$\tau$,此时其值大约为$0.368 \frac{KA}{\tau}$。 其在零点处的切线与X轴的交点恰好为$(\tau,0)$
阶跃响应
考虑阶跃函数$e(t) = e_0 u(t) \iff E(p) = \frac{e_0}{p}$。 则其响应为$S(p) = \frac{K}{1+\tau p} \frac{e_0}{p} \iff s(t) = Ke_0(1 - e^{-t \backslash \tau}) u(t)$ 从而其阶跃响应与目标的差也是一个指数衰减函数,在$3 \tau$时输出约为$0.95 K e_0$。
斜坡函数响应
考虑斜坡函数$e(t) = \alpha t u(t) \iff E(p) = \frac{\alpha}{p^2}$。 其响应为$S(p) = \frac{K \alpha}{p^2(1+\tau p)}$,对应时域函数为$s(t) = K \alpha (t - \tau + \tau e^{-t \backslash \tau})$。 从而其渐近线为从$(\tau,0)$开始的一条斜率为$K \alpha$的直线。 输出在零点处的切线为水平线。
综上,$\tau > 0$的一阶系统总是稳定的,且其响应时间(以相对误差5%计)为$3\tau$。
图像表示
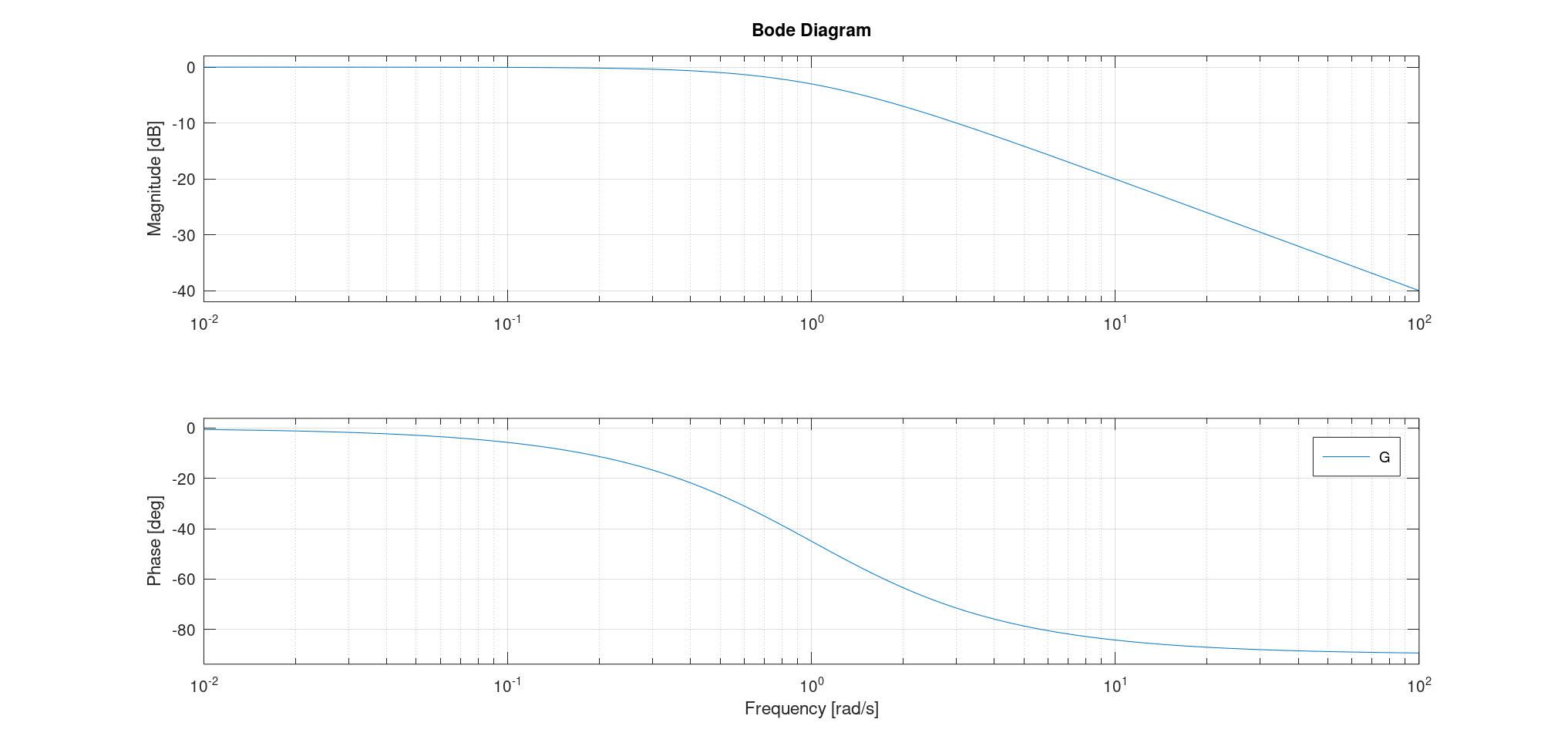
一阶系统的传递函数为: \(H(p) = \frac{K}{1 + \tau p} \implies H( j \omega ) = \frac{K}{1 + \tau^2 \omega^2} - j \frac{K \tau \omega}{1 + \tau^2 \omega^2}\) 从而有 \(\left\{ \begin{aligned} G_{db} ( \omega ) &= 20 \log K - 10 \log (1 + \tau^2 \omega^2) \\ \phi ( \omega ) &= - \arctan (\tau\omega) \end{aligned} \right.\) 在低频区,$G_{db} \sim 20 \log K, \phi = 0^-$; 在高频区,$G_{db} \sim 20 \log K - 20 \log \tau \omega, \phi = - \frac{\pi}{2}$。 从而,低频区的渐近线为水平直线,而高频区的渐近线为斜率为$-20$的直线。 其交点为$\omega = \omega_0 = \frac{1}{\tau}$,称为截止频率或截断频率。 在截止频率处,有$G_{db} = 20 \log K - 10 \log 2 \approx 20 \log k - 3, \phi = -\frac{\pi}{4}$。
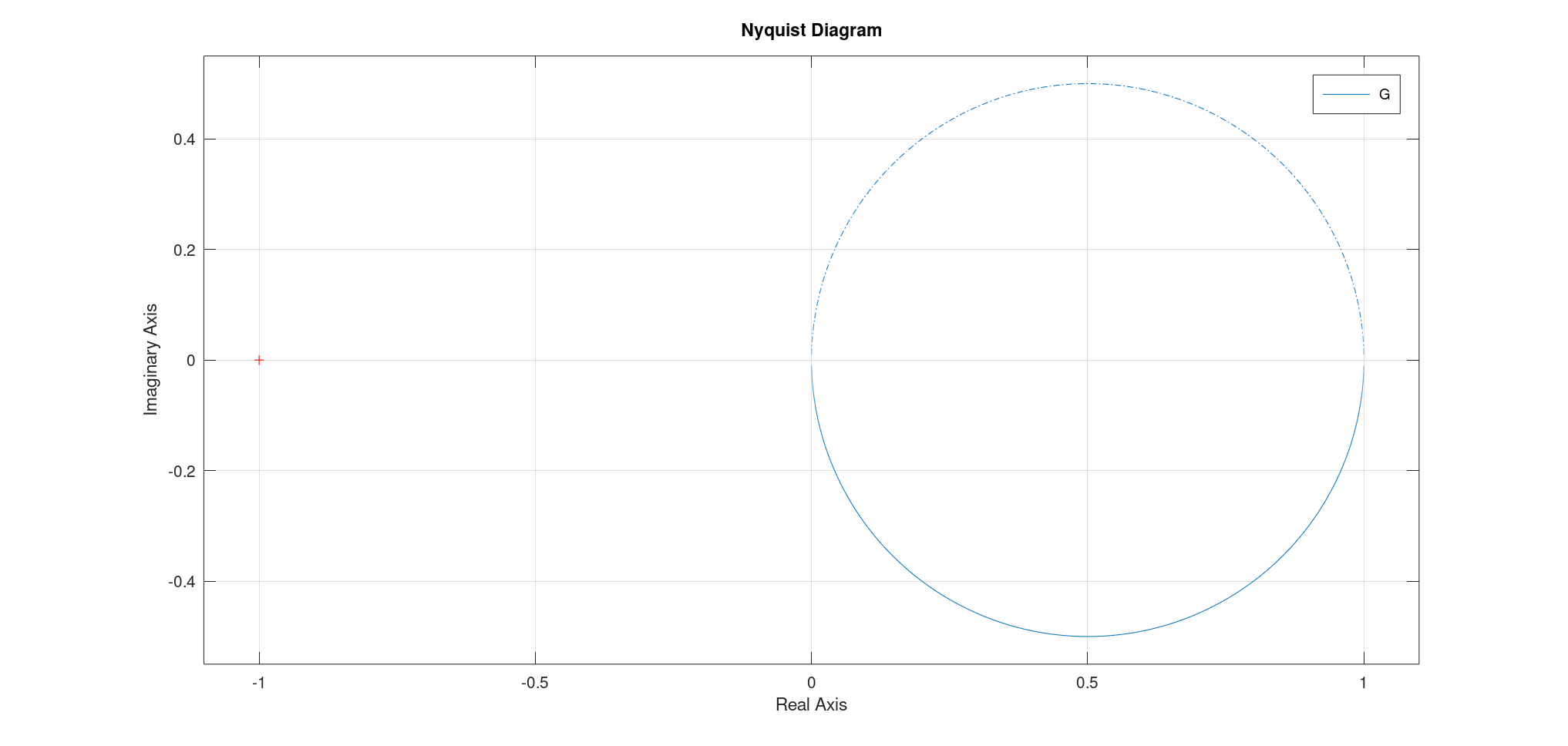
此外我们注意到: \((\Re [ H(j\omega) ] - \frac{K}{2})^2 + (\Im [H(j\omega)])^2 = \frac{K^2}{4}\) 因此其奈奎斯特图为一个圆心在$(-K/2, 0)$的圆。 如果限制$\omega > 0$,则为一个在y负半轴的半圆。
要点:
- 波德图: 增益部分有两条渐近线,交点为截止频率; 此时增益为$20 \log k - 3$,辐角为$-\frac{\pi}{4}$。
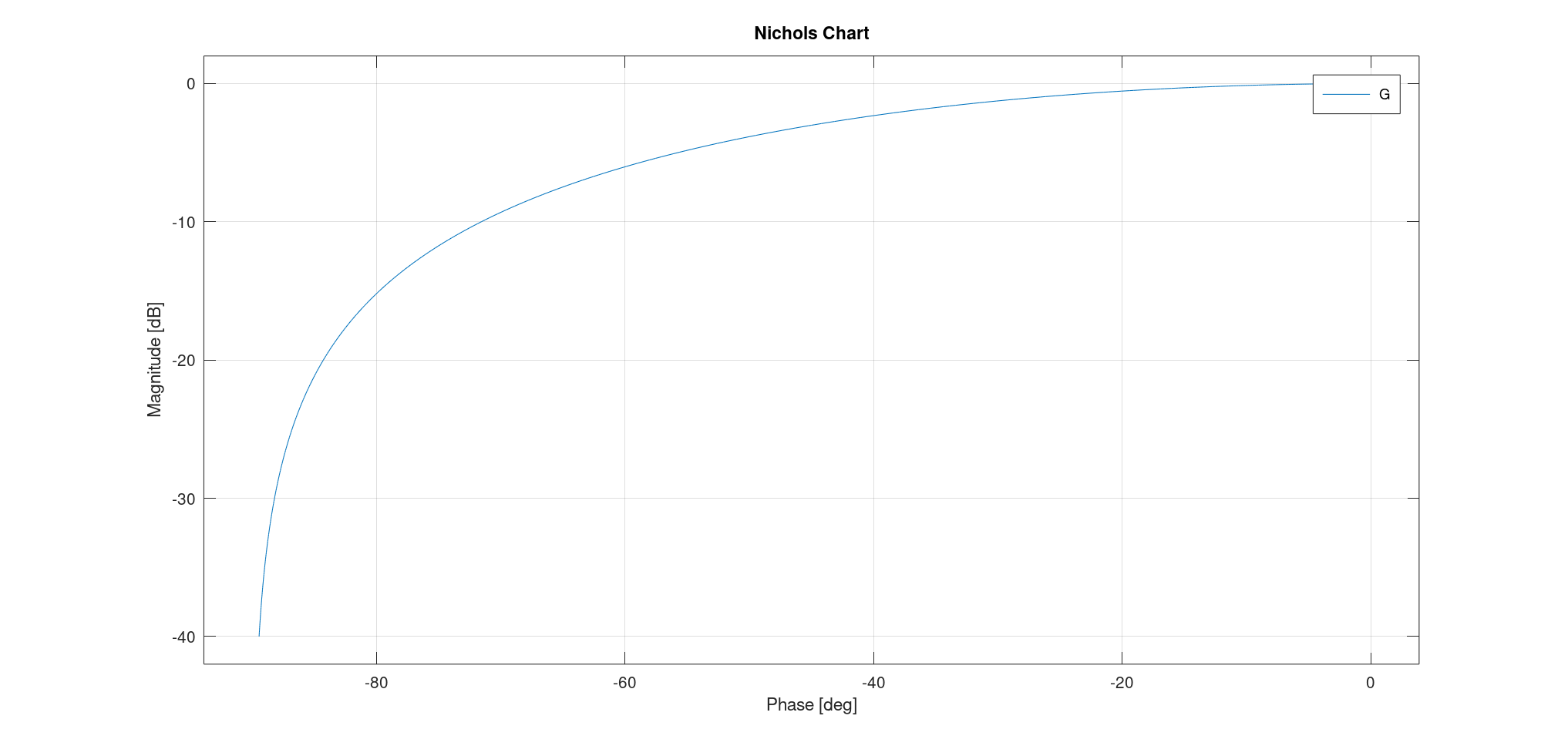
- 尼柯尔斯图: $\omega = 0$时在$(0,20 \log K)$; $\omega = \omega_0$时在$(-45^\circ, 20 \log K - 3)$; $\omega \to \infty$时在$(-90^\circ, -\infty)$。
- 奈奎斯特图: 一个半圆,$\omega = 0$时在$(K,0)$; $\omega \to \infty$时在$(0,0)$。
二阶系统
二阶系统的传递函数为: \(H(p) = \frac{K}{1 + 2 \xi \frac{p}{\omega_0} + \frac{p^2}{\omega_0^2}}\) 其中$\xi$称为阻尼系数,$\omega_0$为截断频率。 传递函数的两个极点(如果存在)可写为以下形式: \(0 = 1 + 2 \xi \frac{p}{\omega_0} + \frac{p^2}{\omega_0^2} = \frac{(p - p_1)(p - p_2)}{\omega_0^2}\) 这个二次多项式函数是否有零点取决于其判别式: \(\Delta = 4 \omega_0^2 (\xi^2 - 1)\) 从而阻尼系数对这个系统有很大的影响。
阶跃响应
我们以不同的阻尼系数分别讨论其阶跃响应,因为阶跃响应最简单。
$\xi = 0$
此时系统有两个共轭的极点:$p_{1,2} = \pm j \omega_0$,输出为: \(S(p) = K e_0 \left( \frac{1}{p} - \frac{p^2}{p^2 + \omega_0^2} \right)\) 在时域上有: \(s(t) = K e_0 \left( 1 - \cos \omega_0 t \right) u(t)\) 即其响应为一个振荡的三角函数,周期为$\frac{2 \pi}{\omega_0}$
$0 < \xi < 1$
此时系统有两个共轭的极点:$p_{1,2} = -\xi \omega_0 \pm j \omega_0 \sqrt{1 - \xi^2}$。 \(S(p) = \frac{K}{1 + 2 \xi \frac{p}{\omega_0} + \frac{p^2}{\omega_0^2}} \frac{e_0}{p}\) 我们设$\omega_p = \omega_0 \sqrt{1 - \xi^2}, \sigma = \xi \omega$,则有: \(S(p) = K e_0 \left[ \frac{1}{p} - \left( \frac{p + \sigma}{(p+\sigma)^2 + \omega_p^2} + \frac{\sigma}{(p+\sigma)^2 + \omega_p^2} \right) \right]\) 此时有: \(s(t) = K e_0 \left[ 1 - \frac{e^{-\xi \omega_0 t}}{\sin \varphi} \sin \left( \omega_0 \sqrt{1-\xi^2} t + \varphi \right) \right] u(t)\) 其中$\sin \varphi = \sqrt{1 - \xi^2}, \cos \varphi = \xi$。 则其输出为一个指数衰减的三角函数,周期为$\frac{2 \pi}{\omega_0 \sqrt{1-\xi^2}}$。 由拉普拉斯变换的性质,我们知道$\dot s (0^+) = 0$,从而其在原点处的切线水平。
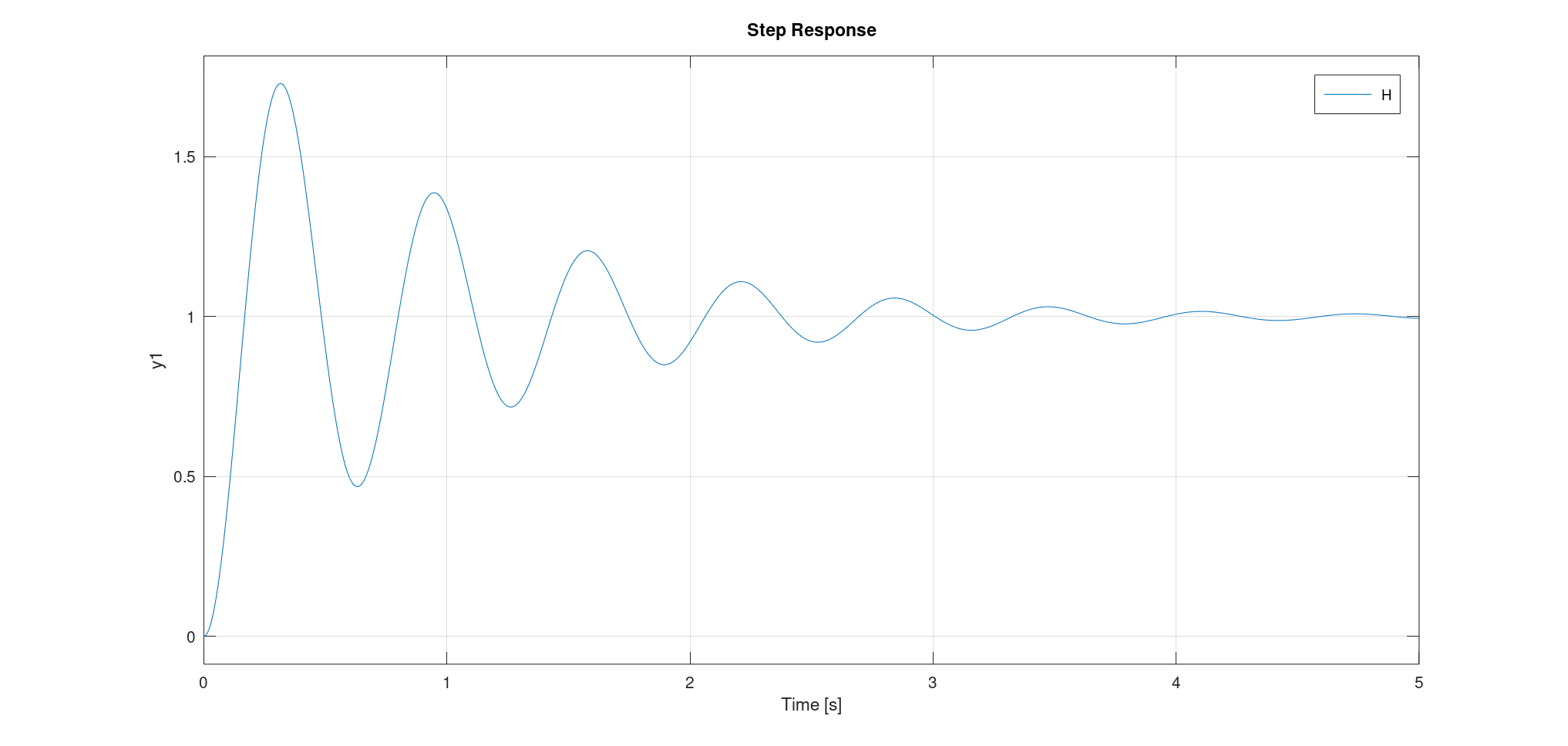
我们注意到函数的极值是也是指数衰减的,第n个极值的绝对值为$|D_n| = K e_0 \exp \left[ - \frac{\xi \pi}{\sqrt{1 - \xi^2}} n \right]$。 我们定义$D_{n\%} = \left| \frac{D_n}{K e_0} \right|$。 从而$D_{n\%} = (D_{1\%})^n = \exp \left[ - \frac{\xi \pi}{\sqrt{1 - \xi^2}} n \right]$。 这个值可以用来确定系统的阻尼系数。
$\xi = 1$
此时系统有两个相同的极点:$p = - \omega_0$。 输出为: \(S(p) = K e_0 \left[ \frac{1}{p} - \frac{1}{p + \omega_0} - \frac{\omega_0}{(p + \omega_0)^2} \right]\) 时域输出为: \(s(t) = K e_0 \left[ 1 - \exp (-\omega_0 t) - \omega_0 t \exp ( - \omega_0 t ) \right] u(t)\) 系统不存在振荡。
$\xi > 1$
此时系统有两个实极点:$p_{1,2} = - \xi \omega_0 \pm \omega_0 \sqrt{\xi^2 - 1}$。 我们设$\omega_a = \omega_0 \sqrt{\xi^2 - 1}, \sigma = \xi \omega$,有: \(S(p) = K e_0 \left[ \frac{1}{p} - \left( \frac{p + \sigma}{(p + \sigma)^2 - \omega_a} + \frac{\sigma}{(p + \sigma)^2 - \omega_a} \right) \right]\) 时域上: \(s(t) = K e_0 \left[ \frac{e^{-\xi \omega_0 t}}{\sqrt{\xi^2 - 1}} \left( \sqrt{\xi^2 - 1} \cosh (\omega_a t) + \xi \sinh (\omega_a t) \right) \right] u(t)\)
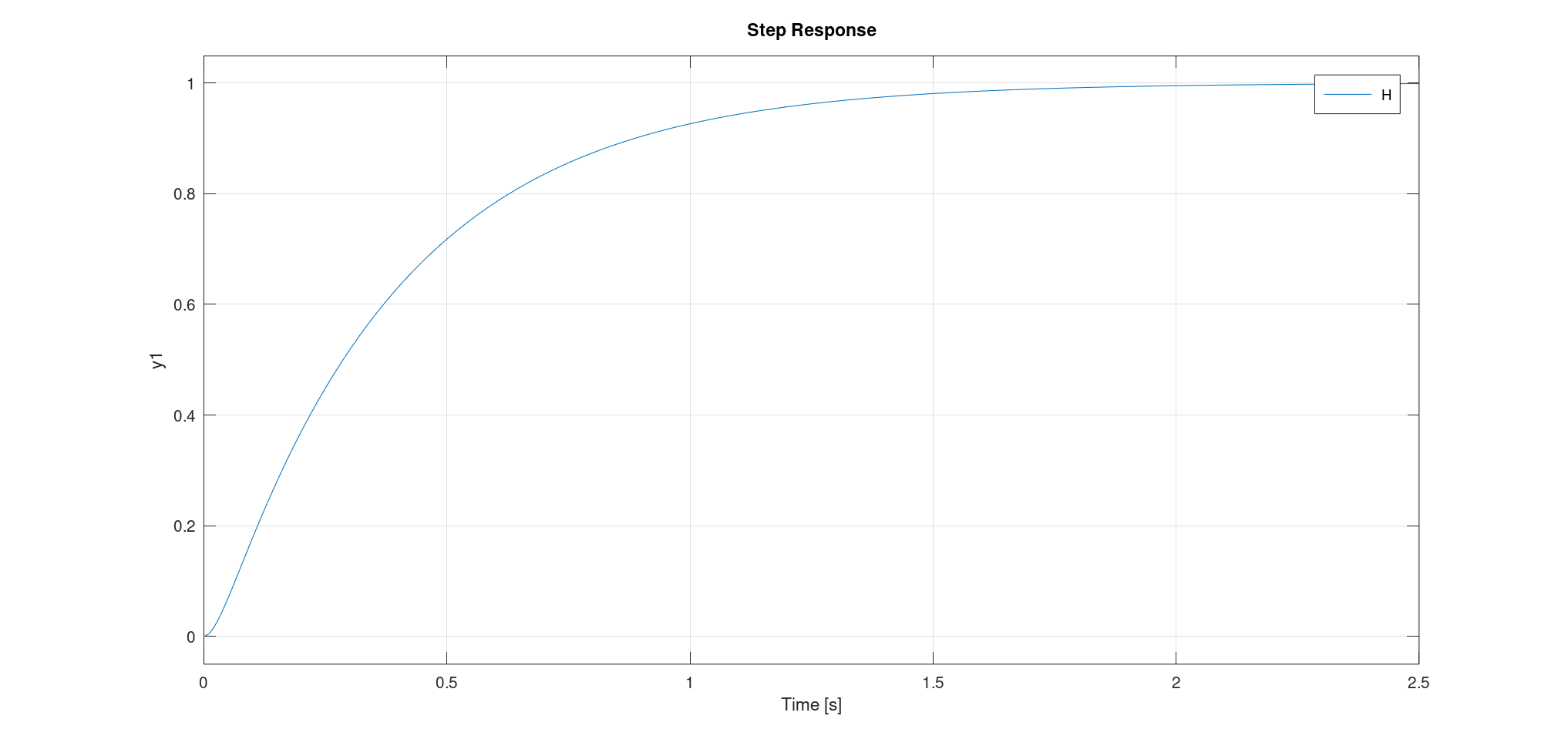
此时我们注意到这个系统也可以拆成两个一阶的系统: \(H(p) = \frac{K}{1 + \frac{2 \xi}{\omega_0} p + \frac{p^2}{\omega_0^2}} = \frac{K \omega_0}{(p - p_1)(p - p_2)} = \frac{K}{(1 + \tau_1 p)(1 + \tau_2 p)}\)
若有$\tau_1 \gg \tau_2$,则我们可以有两种方法来用一阶系统逼近:
- 设$\tau_2 = 0$,则$H(p) = \frac{K}{1 + \tau_1 p}$;
- 令$\tau_2 \to 0$,则$\frac{1}{1 + \tau_2 p} \sim 1 - \tau_2 p \sim e^{- \tau_2 p}$ 此时$H(p) = \frac{K}{1 + \tau_1 p} e^{-\tau_2 p}$。这个系统称为迟滞一阶系统。
响应时间与阻尼系数
我们知道,系统的响应时间可由到达其稳定输出5%左右的时间来表示。 二阶系统的响应时间和其阻尼系数之间存在较为复杂的关系。
有两处特殊的值需要注意:
- $\xi = 1$,此时系统处于临界状态,响应时间在不振荡的条件下最短,$t_{5\%} = \frac{4.744}{\omega_0}$;
- $\xi = 0.69$,此时系统略有振荡,但响应时间最短,$t_{5\%} = \frac{2.859}{\omega_0}$。 实际上,此时有$D_{1\%} = 4.99999\%$。
图像表示
和阶跃响应相同,我们也要按照阻尼系数来分类讨论。 有: \(H(p) = K (1 + \frac{2\xi}{\omega_0} p + \frac{1}{\omega_0^2} p^2)^{-1} \implies H(j\omega) = K (1 - \frac{\omega^2}{\omega_0^2} + 2 j \frac{\xi \omega}{\omega_0})^{-1}\) 从而 \(\left\{ \begin{aligned} A(\omega) &= \frac{K}{\sqrt{(1 - \frac{\omega^2}{\omega_0^2})^2 + 4 \frac{\xi^2 \omega^2}{\omega_0^2}}} \\ \varphi(\omega) &= - \arg \left[ 1 - \frac{\omega^2}{\omega_0^2} + 2 j \frac{\xi \omega}{\omega_0} \right] \end{aligned} \right.\)
先来看辐角。 对于辐角来说,一个重要的问题是这个复数的实部的符号是不确定的,从而反三角函数$\arctan$的计算比较困难。 我们把这个复数乘以虚数单位$j$,相当于旋转了$90^\circ$,同时把不确定符号的实部变为虚部,而恒正的虚部变为实部。 从而我们有: \(\varphi(\omega) = - \frac{\pi}{2} + \arctan \left( \frac{\omega_0^2 - \omega^2}{2 \xi \omega \omega_0} \right)\)
再来看增益。 我们有: \(\begin{aligned} G_{dB} (\omega) &= 20 \log A \\ &= 20 \log K - 10 \log \left[ \left( 1 - \frac{\omega^2}{\omega_0^2} \right)^2 + 4 \frac{\xi^2 \omega^2}{\omega_0^2} \right] \\ \end{aligned}\) $\omega = \omega_0$时: \(G_db (\omega_0) = 20 \log K - 20 \log \frac{1}{2 \xi}\) 我们记$Q = \frac{1}{2 \xi}$,称为品质因数。
我们继续研究增益的极值。 对于一阶系统,增益是单调的,但是对二阶系统,其可能出现极大值。 我们令$f(\omega) = (1 - \frac{\omega^2}{\omega_0^2})^2 + 4 \frac{\xi^2 \omega^2}{\omega_0^2}$。 这个函数是增益的分母,从而我们需要知道它的极小值。 求导可得: \(f^\prime (\omega) = 4 \frac{\omega}{\omega_0} (-1 + \frac{\omega^2}{\omega_0^2} + 2\xi^2)\) 从而其在$\omega = \omega_0 \sqrt{1 - 2 \xi^2}$处取最小值。
如果$\xi < \frac{\sqrt{2}}{2}$,则其存在共振现象,共振频率为$\omega_r = \omega_0 \sqrt{1 - 2 \xi^2}$。 此时其增益为 \(G_{dB} = 20 \log K - 10 \log \left[ 4\xi^2 + 4\xi^2 (1 - 2\xi^2) \right] = 20 \log K + 20 \log \frac{1}{2\xi \sqrt{1 - \xi^2}}\) 我们定义$Q_S = \frac{1}{2\xi \sqrt{1 - \xi^2}}$,称为共振因子。
最后,我们研究一下渐近线。 渐近线的研究方法和一阶系统相同。
- $\omega \to 0$时,增益为一根水平直线,值为$20 \log K$。$\varphi(\omega) = 0$。
- $\omega \to \infty$时,增益为一根斜率为$-40$的直线。$\varphi(\omega) = - \pi$。
- 两根渐近线相交于$\omega_0$,$\varphi(\omega_0) = -\frac{\pi}{2}$。
总结一下要点:
- 波德图:
- 渐近线见上;
- $\omega_0$处,增益值为$20 \log K + 20 \log Q$,辅角为$\varphi(\omega_0) = -\frac{\pi}{2}$;
- 如果$\xi < \frac{\sqrt{2}}{2}$,则存在共振,此时波德图上有极大值点:$(\omega_0 \sqrt{1 - 2 \xi^2}, 20 \log K + 20 \log Q_S)$。
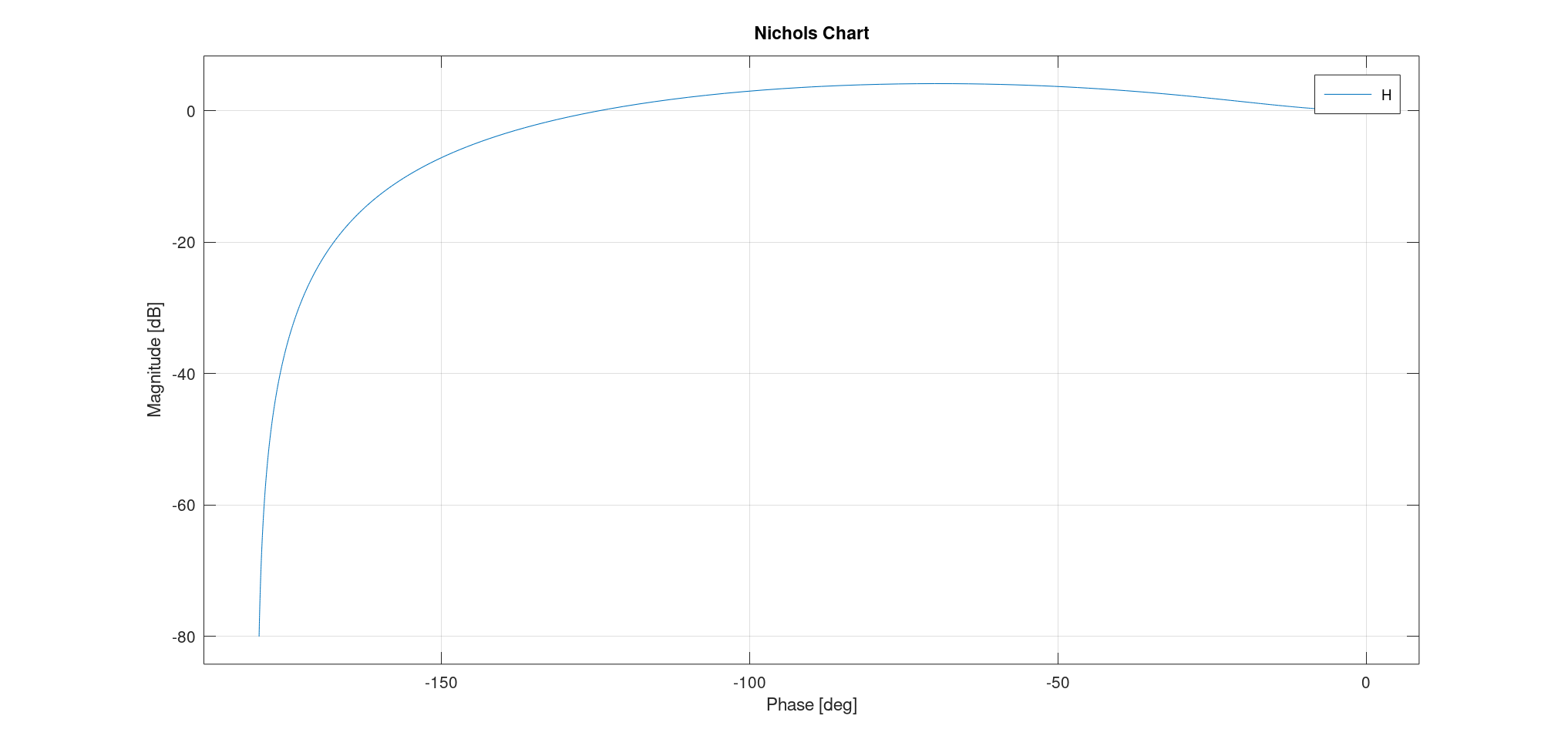
- 尼柯尔斯图:
- 通过两个点:共振频率(共振频率小于截止频率,其辐角大于$- \frac{\pi}{2}$)、截止频率;
- 两条渐近线:$\omega \to 0, \varphi = 0, G_{dB} = 20 \log K$,$\omega \to +\infty, \varphi = - \pi, G_{dB} = - \infty$。
- 奈奎斯特图:
- 通过两个点:共振频率(第四象限,模长大于$K$)、截止频率(交于虚轴负半轴,交点为$(KQ,0)$);
- 起止点:从$\omega \to 0, (K, 0)$出发,至$\omega \to \infty, (0, 0)$结束
$0 < \xi < \frac{1}{2}$


$\xi = \frac{1}{2}$

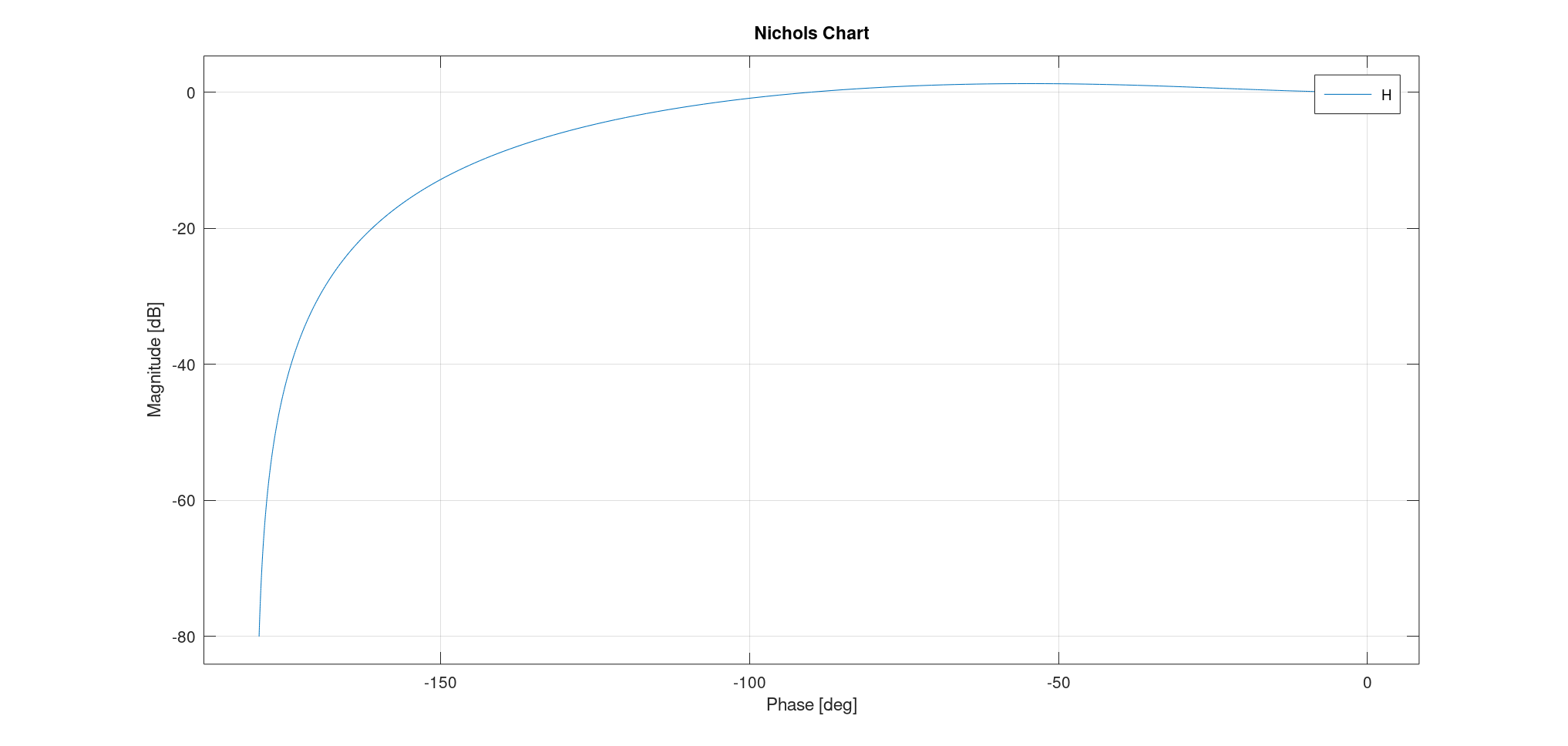

$\frac{1}{2} < \xi < \frac{\sqrt{2}}{2}$
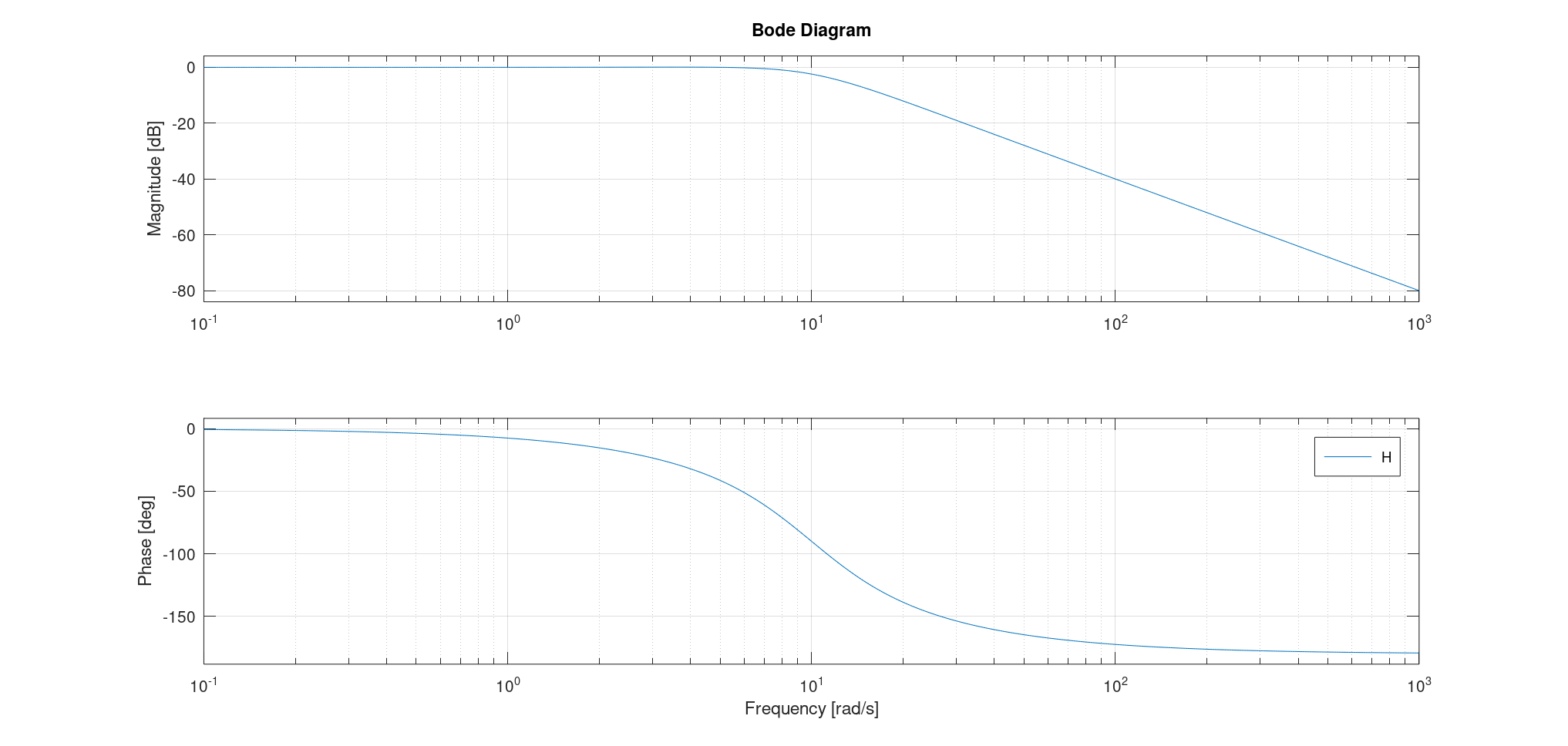
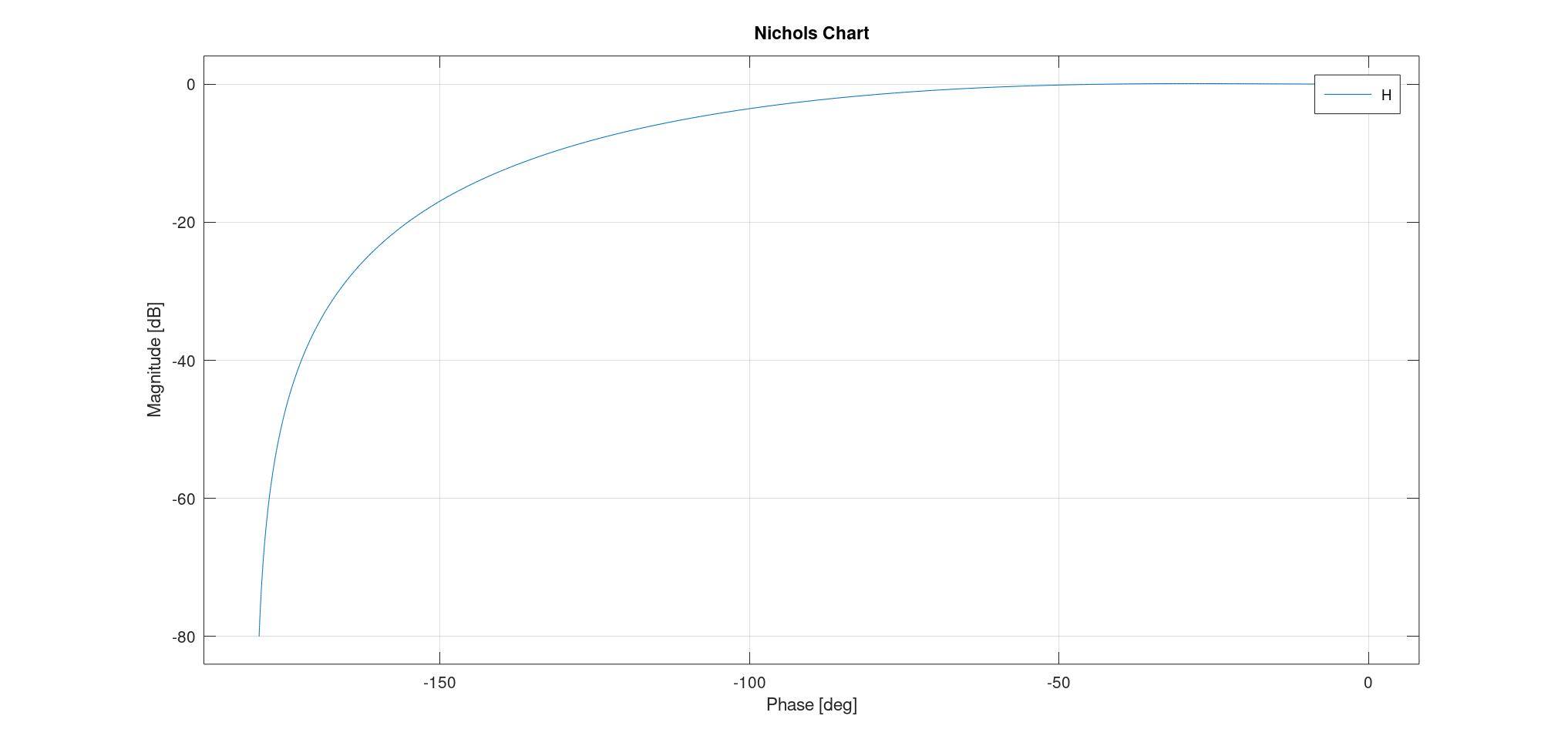
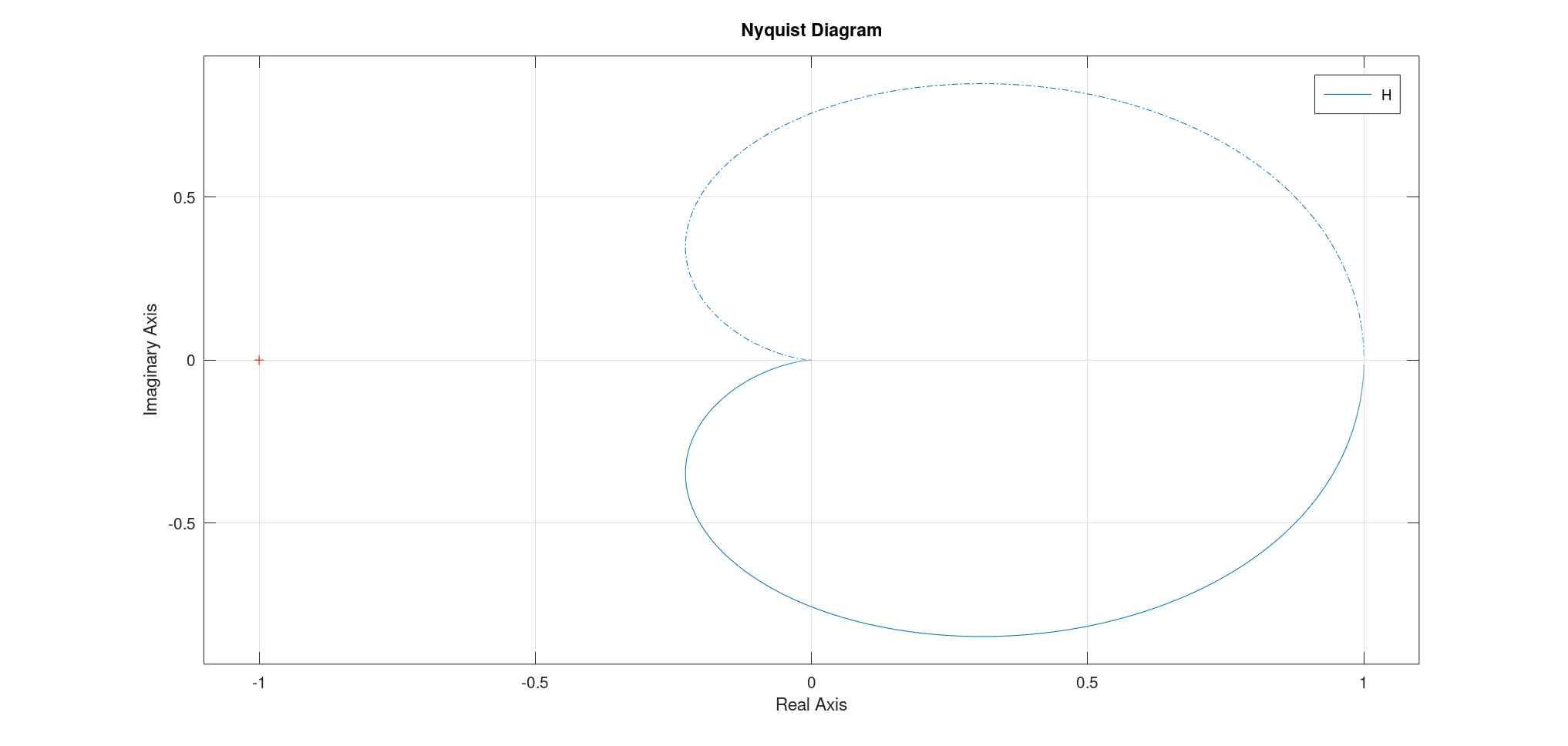
$\frac{\sqrt{2}}{2} < \xi < 1$
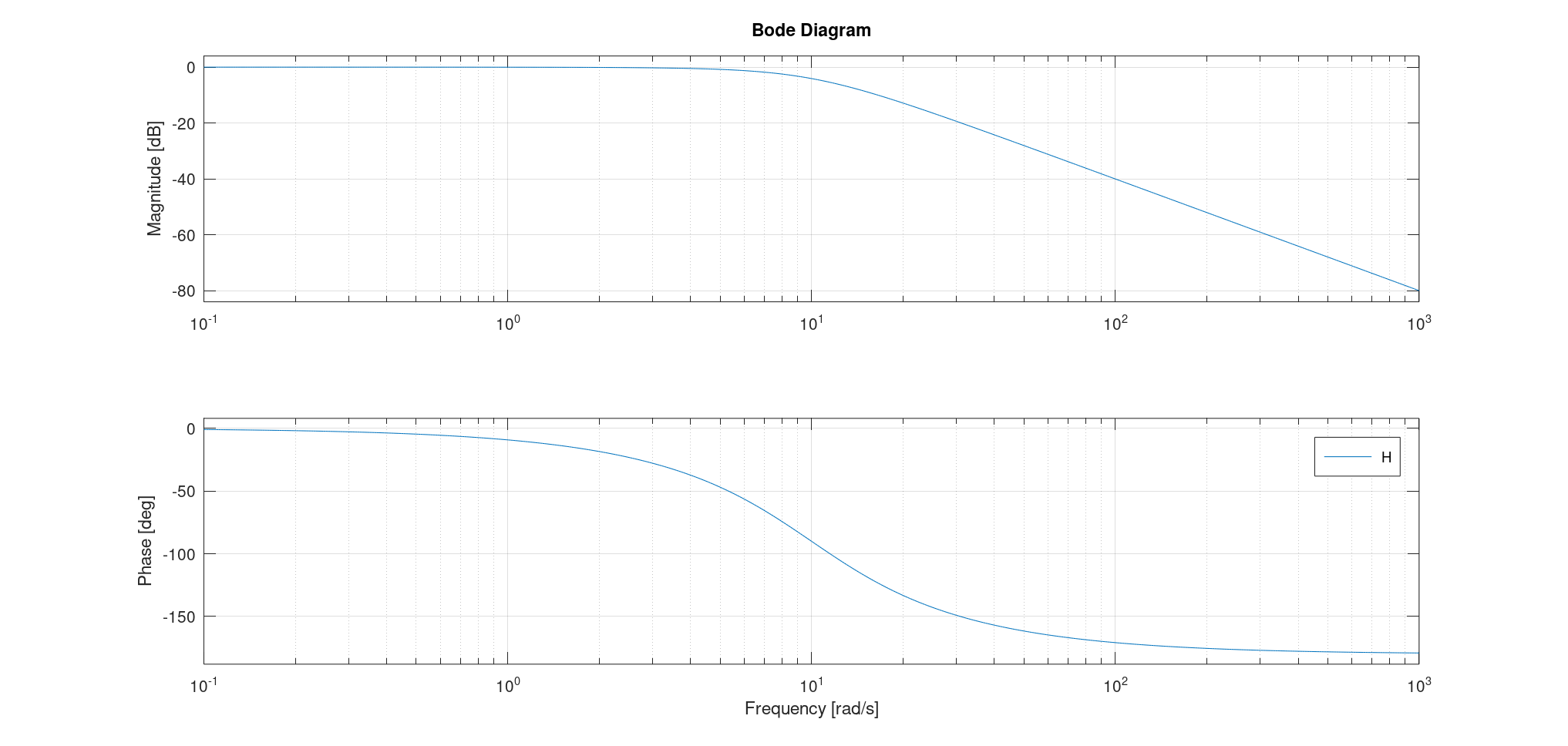

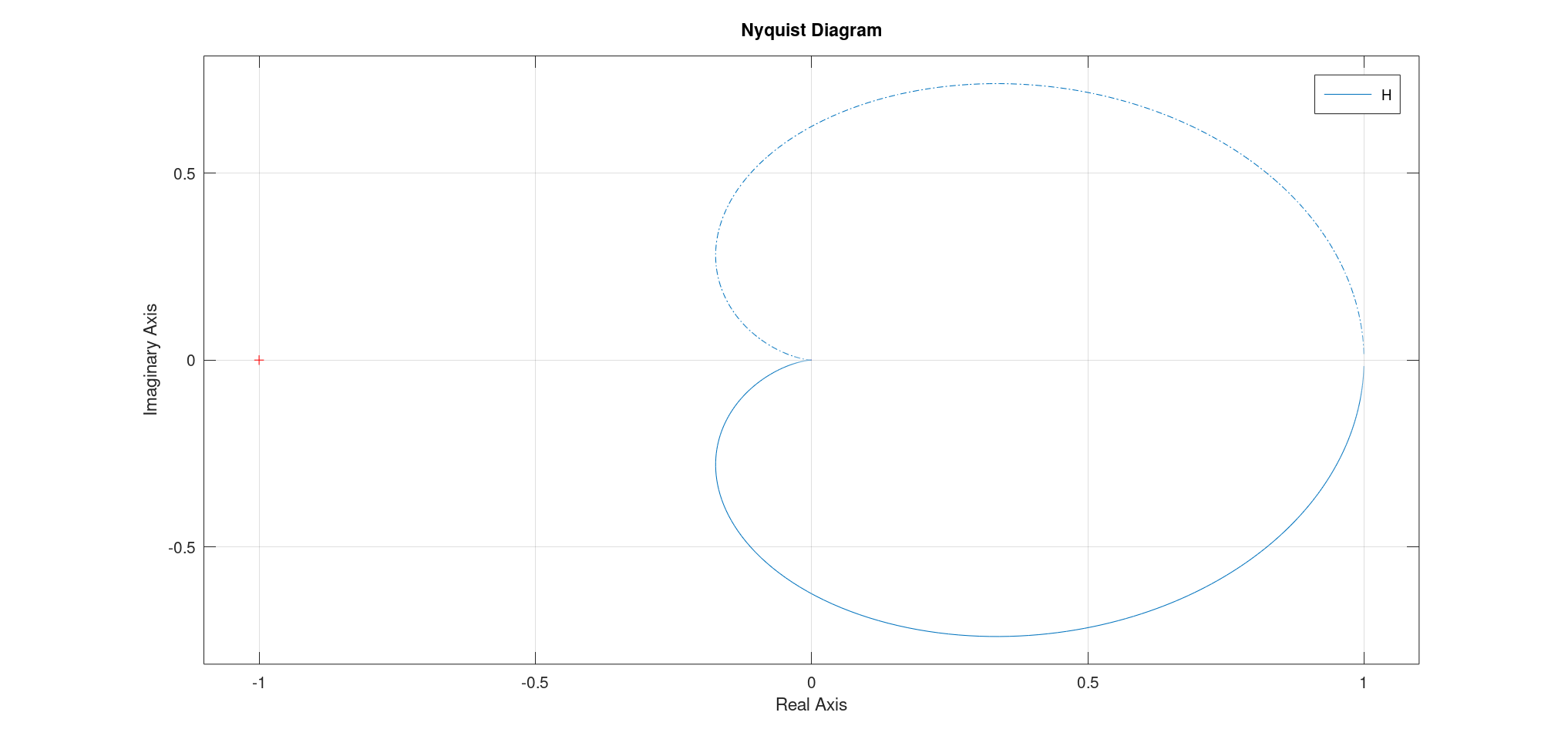
$1 < \xi$
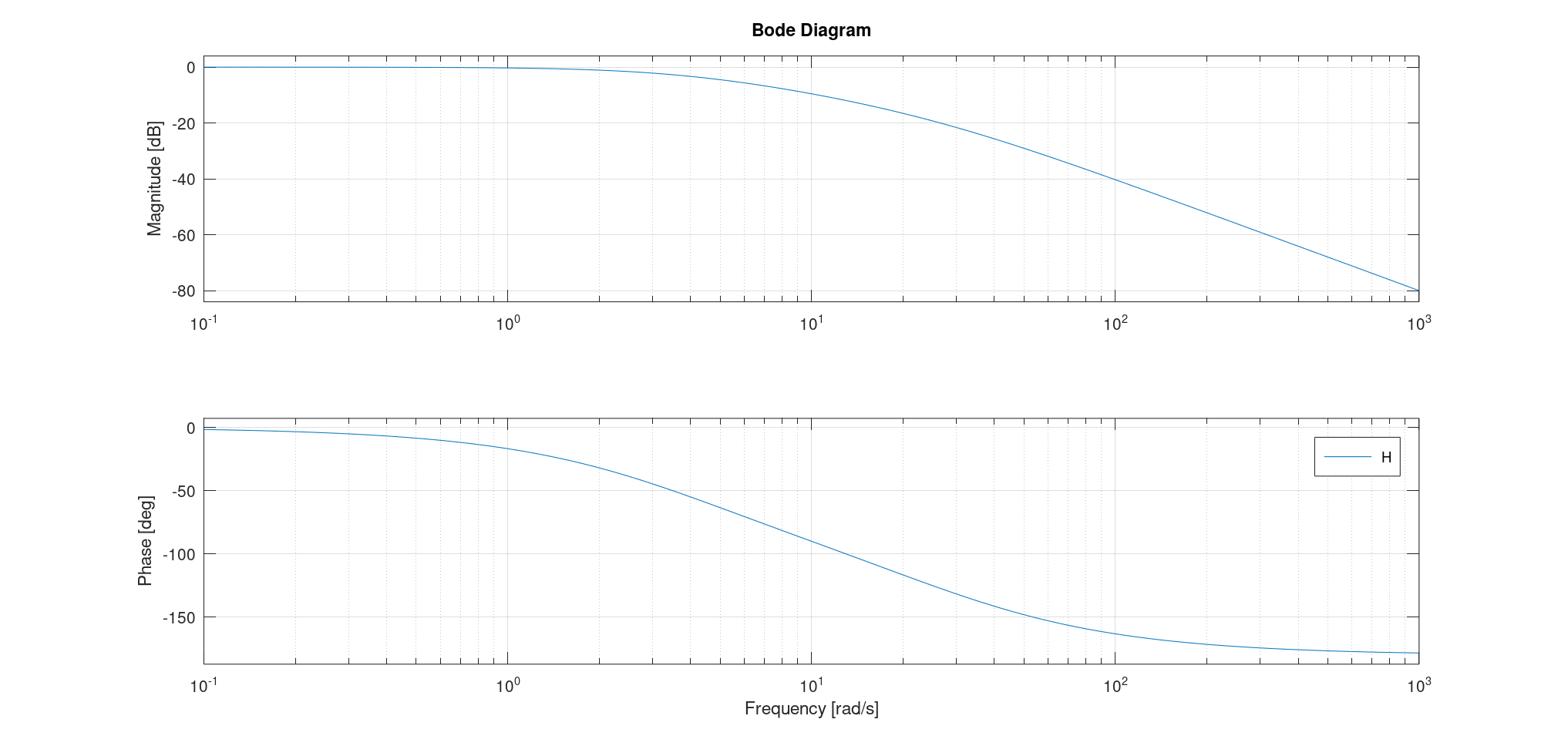
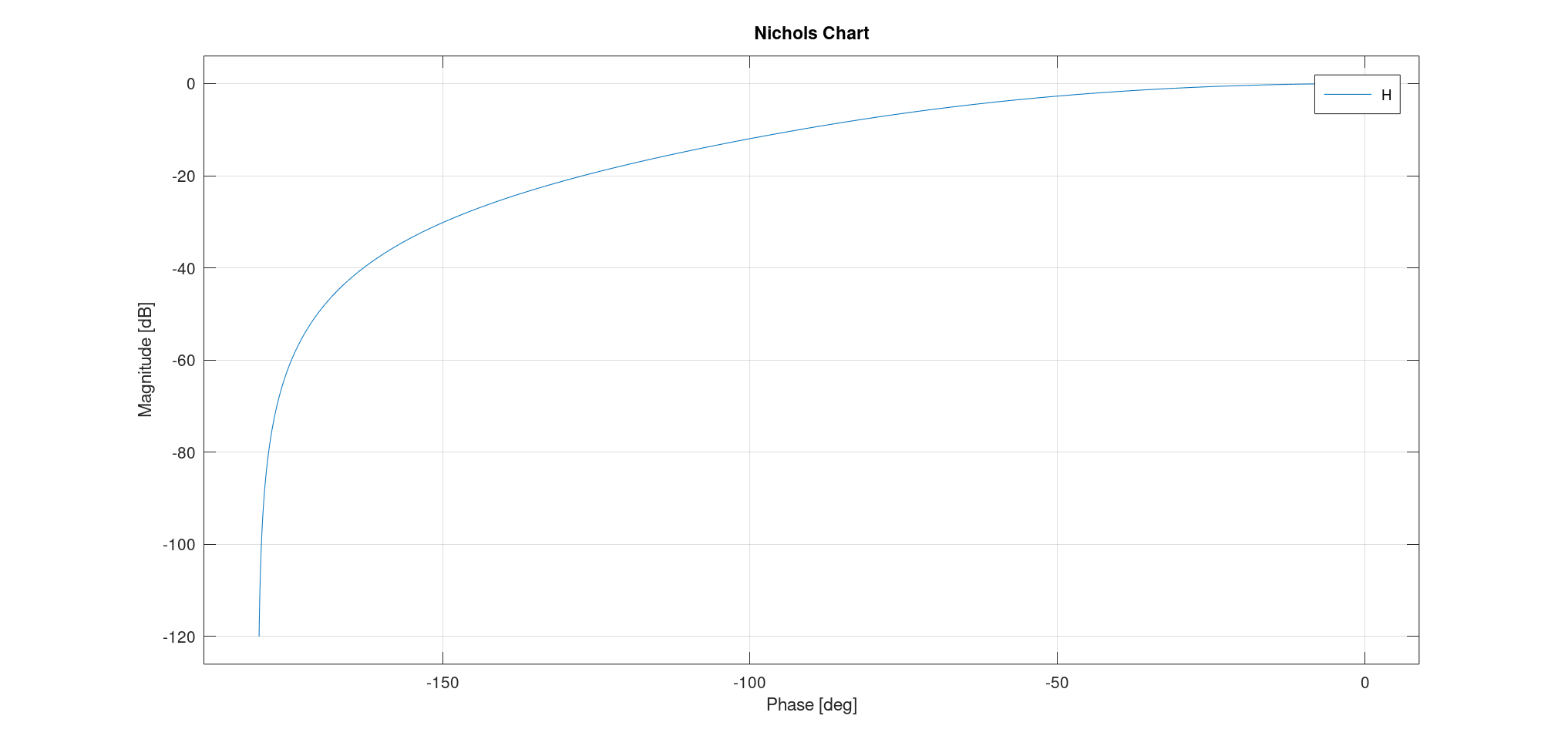
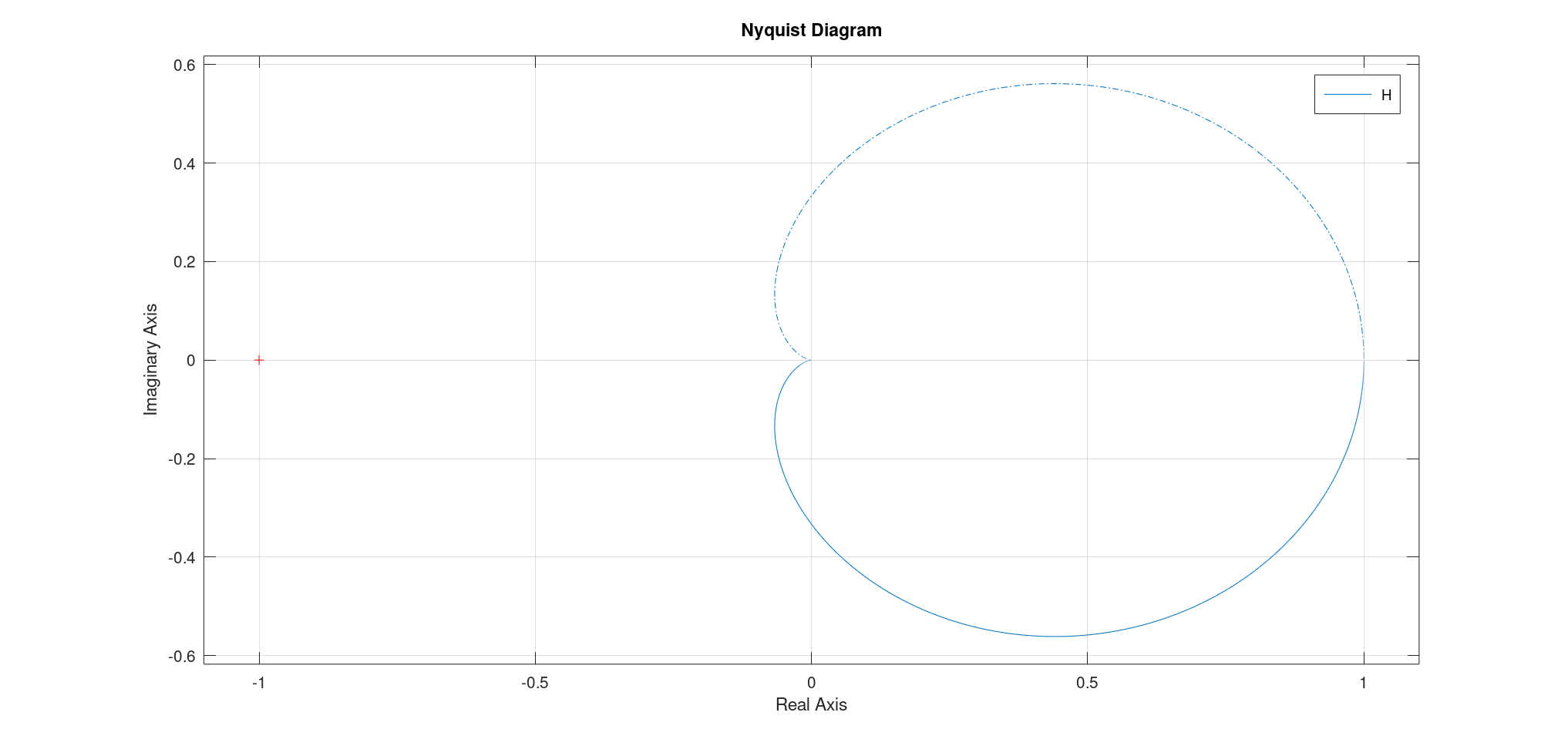
特别注意,在此情况下,该二阶传递函数可被分解成两个一阶的传递函数,从而有三条渐近线: 一条水平直线;一条斜率为-20的直线,这是一阶系统的渐近线;一条斜率为-40的直线。