双相系统
在本文中,我们将考察相变之中的纯净物系统。
本文中凡是小写字母表示的物理量,如不加特殊说明,那么表示对应大写字母物理量的单位质量形式。
相
所谓“相”,就是指在系统当中所有强度参数都是连续函数的区域。 一个相可以是均匀的,也可以是不均匀的。 比如说水和水蒸气的混合体系,如果考虑某个点处的密度,那么这个函数在水汽界面处是断开的。
通常物体具有四个相:固相、液相、气相和超临界相。 固相分子密集有序排列,液相分子密集无序排列,气相分子则非常分散。 通常我们认为固体和液体是不可压缩(体积与压强无关)、不会膨胀(体积与温度无关)的。 当温度和压强都较高时,气体和液体之间不存在明显的界限,此时我们称系统处于超临界状态。
对于固体,还存在同素异形体这一特殊现象,这是固体的晶体结构不同导致的。 这些同素异形体的理化性质通常不同,因此也可以视为不同的相。
相图
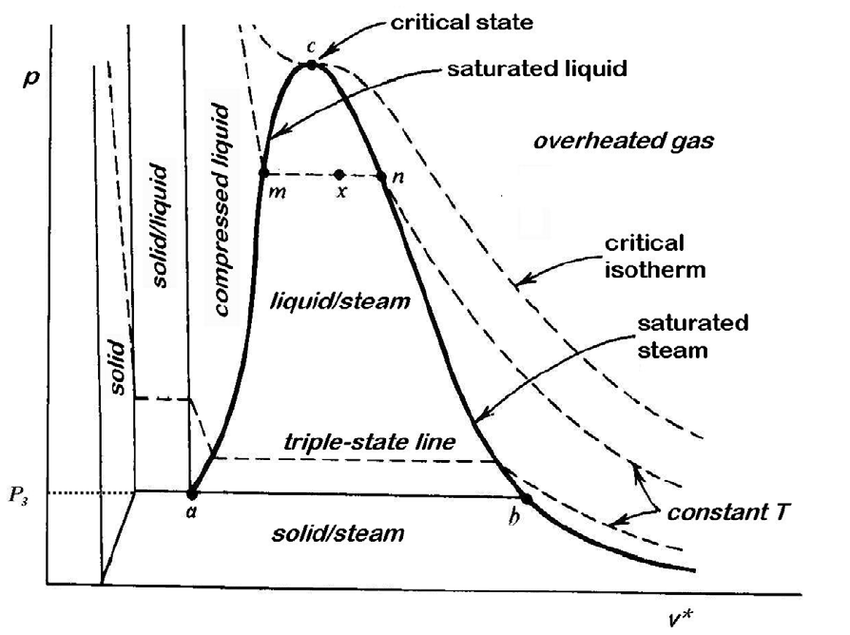
上面是一张典型的相图,虚线部分是水的固液分界线,实线部分是通常情况。 相图上最重要的部分就是“四区”、“三线”、“两点”。
- 四区指分别代表固态、液态、气态和超临界态的四个区域;
- 三线指固液气三态之间的分界线;
- 两点指三相点(即三线交叉之处)和临界点。
如果系统的温度和压强处于三线上,那么系统可能处在混合态,也可能在任何一态下。
相变
我们通过在比三相点压强更高,温度更低的状态恒压加热系统,可以让系统依次经过固液气三态。 通过向系统输入能量,我们可以注意到,系统的温度先是上升,然后在发生相变时保持不变,相变完全后再重新上升。 如果我们在相变过程中停止加热,可以注意到系统仍能维持平衡。 这种平衡叫做相平衡。 这种平衡的出现意味着系统在某一压强下维持相平衡的温度是唯一的; 同理,在某一温度下维持相平衡的压强也是唯一的。
相变潜热
系统在两个相之间发生相变时,虽然温度不变,但是显然与外界发生了能量交换。 考虑到系统虽然没有非体积功,但是仍会发生体积变化,因此我们用焓而非内能刻画这一变化。 设系统在前一相的焓为$H_A$,后一相的焓为$H_B$,那么有: \(\newcommand\d{\mathrm{d}} H_B = H_A + Q_{A \to B} + \underbrace{\int V \d P}_{\text{等压变换}} = H_A + Q_{A \to B}\) 显然两个相之间的焓是不连续的,这个焓的差值就是两个相之间的相变潜热。 我们采用等压变化的假设,是因为通常情况下相变是在大气压下缓慢发生的。
两个相A、B之间的相变潜热定义为: \(L_{A \to B} = H_B - H_A \qquad l_{A \to B} = h_B - h_A\) 后一式子是单位质量的形式。 若该相变是恒压的,那么有: \(\delta Q = l_{A \to B} \delta m\)
通常情况下,系统从液态变为气态(汽化、液化)的潜热远大于从固态变为液态(熔化、凝固)的。
我们知道,对于等压变化,有$\Delta S = \frac{Q}{T} = \frac{\Delta H}{T}$,从而,气体的熵远大于液体的,液体的远大于固体的。
气液平衡
我们把一些固定质量的液态水从气态缓慢恒温加压到液态,记录系统的体积和压强之间的关系,可以得到下图。
从右往左观察穿过气液平衡态的那根曲线。
- n点右侧,系统处于气态,遵守$PV = \text{常数}$。
- n点到m点之间,系统处于气液混合态,n点称为露点,m点称为沸点。
- m点右侧,系统处于液态,由于液体不可压缩,曲线非常陡峭。
在相变之时,系统的体积持续减小,但是压强并不改变。 这一压强称为系统的饱和蒸汽压。
质量分数
在PT图中,相变仅仅只有一个点;而在PV图中,相变有整整一段直线。 这条直线上的每一个点都对应一个液相(或气相)的质量分数。
我们定义$m_g,m_l$分别表示在气态和液态的质量;$v_g,v_l$分别表示两态的单位质量体积(密度的倒数),有: \(M = m_l + m_g , \; V = m_l v_l + m_g v_g\)
我们可以定义质量分数:
相$i$的质量分数表示为: \(x_i = \frac{m_i}{M}\) 对于纯净物系统,质量分数和摩尔分数相同。 由于质量守恒,任何双相系统满足$x_1+x_2 = 1$。
通过把体积重新写成两相体积之和,我们可以证明以下命题:
设系统的沸点为$L$,露点为$G$,当前在PV图上的点为$N$,那么有 \(x_l = \frac{NG}{LG} \quad x_g = \frac{LN}{LG}\)
不难看出,随着系统沿线段向左变化,液体的质量分数变大,气体的质量分数变小。
实际上,我们有以下更强的命题:
任何双相系统的强度参数都可由两个相的对应强度参数和质量分数表示: \(X(P,T,x_1) = x_1 X_1(P,T) + x_2 X_2(P,T)\)
分压与蒸发
对于一混合系统(如空气),我们定义其组分的分压等于总压乘其摩尔分数: \(P_i = \frac{n_i}{n_{tot}} P_{tot}\) 显然,对只有一个组分的系统,其分压等于总压。
我们已经知道,在某一温度下,只有组分的分压等于其饱和蒸汽压时,系统才能平衡。 因此,若组分的分压小于其饱和蒸汽压,这一组分会一直汽化;若大于,则这一组分会一直液化。 这也是晾干衣服的原理,也就是说,晾干衣服时系统实际上没有达成热力学平衡。 倒过来说,也可以说正因为系统没有达成平衡,才能晾干衣服。
纯净物的相变
我们已经知道,发生相变前后,系统的焓和熵都是不连续的。 如果相变是等压的,那么相变潜热恰好等于其吸收或放出的热量。 对于熵,如果相变是等压且准静止的,那么有$s_2-s_1=\frac{l_{1 \to 2}}{T}$。
克拉佩龙方程
克拉佩龙方程提供了计算相变潜热的方法:
单位质量(或单位物质的量)的相变潜热由以下方程确定: \(l_{1 \to 2} = h_2(T) - h_1(T) = T(v_2 - v_1) \frac{\d P_{\text{平衡}}(T)}{\d T}\)
这个方程的证明较为复杂,此处不在赘述。
温熵图
由温度和熵之间的关系画成的图称为温熵图,温熵图中通常还有许多辅助线。
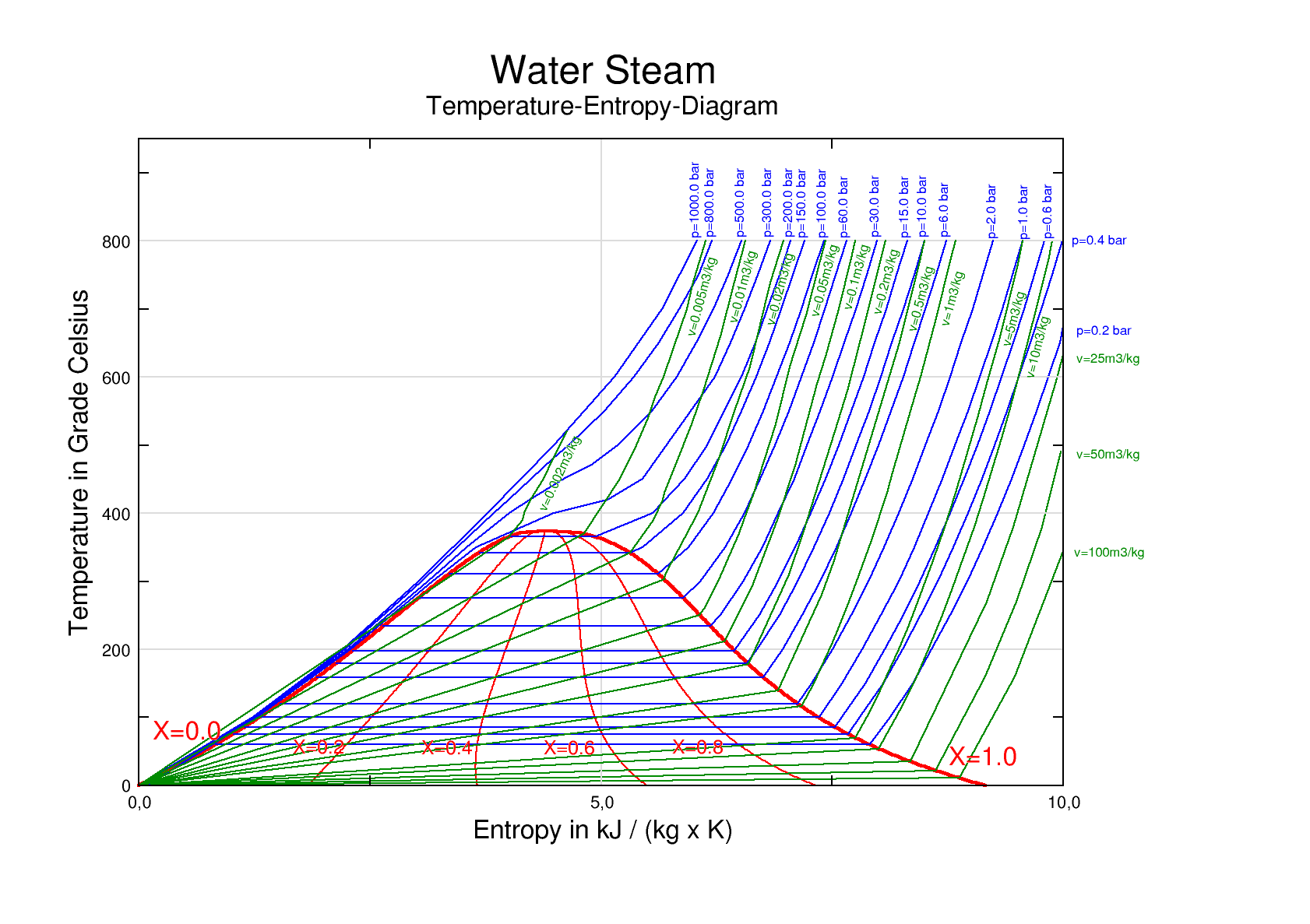
等压线(蓝色):等压线($\d P = 0$)指数上升。 \(\d h = c_p \d T = T \d s + v \d P \implies \frac{\d T}{T} = \frac{\d s}{c_p} \implies T = A e^{\frac{s-s_0}{c_p}}\)
等容线(绿色):等容线($\d v = 0$)指数上升。 \(\d u = c_v \d T = T \d s - P \d v \implies T = B e^{\frac{s-s_0}{c_v}}\)
等焓线(图中未标出):等焓线是双曲线的一支。 \(\d s = \frac{\d h}{T} - \frac{v}{T} \d P \implies \d s = - \frac{v}{T} \d P\)
等分数线(红色): \(x = \frac{s - s_l}{s_v - s_l}\)
例题
已知液态水的比热为$c = 4.2 J/(g \cdot K)$,其单位体积质量忽略不记。 气态水的比热为$c^\prime = 2.0 J/(g \cdot K)$,可视为理想气体,绝热指数$\gamma = 1.3$。 一百摄氏度,一大气压强下汽化的潜热为$l = 2.26 \times 10^3 kJ/kg$。 向大气压下一含有一克150摄氏度水的绝热活塞中加入一克10摄氏度的水,求平衡状态和熵变。
一克水从10度加热到100度需要的热量为: \(\delta Q = c \Delta T = 378 J\) 从150度降温到100度释放的热量为: \(\delta Q = c^\prime \Delta T = -100 J\) 从而降温释放的热量比升温需要的热量更多。 因此系统至少经历两个过程:热交换和相变。 又注意到一克水的液化的相变潜热大于加热所需的能量,因此系统在气液混合态平衡。
- 第一个过程: \(\begin{aligned} \delta Q_\text{汽} + \delta Q_\text{液} = 0 \\ m c (T - 10) + m c^\prime (100 - 150) = 0 \\ T = 33.8 ^\circ C \end{aligned}\)
- 第二个过程: \(\begin{aligned} \delta Q_\text{液} + x l = 0 \\ m c (100 - T) - x \cdot 2260 = 0 \\ x = 0.12 \\ m = 0.12 g \end{aligned}\) 因此系统有0.12克水汽化了。
注意此题中我们隐含地使用了热力学第一定律来证明焓变等于热量。
- 液体升温的熵变: \(\Delta S = m c \ln \frac{T_2}{T_1} = m c \ln \frac{373.15K}{285.15K} = 1.16 J/K\)
- 气体降温的熵变: \(\Delta S = m c^\prime \frac{T_2}{T_3} = - 0.251 J/K\)
- 相变的熵变: \(\Delta S = \frac{Q}{T} = \frac{-x l}{T} = -0.727 J/K\) 从而总的熵变为$0.19 J/K$。